Prove that volume of a parallelopiped with coterminal edges as ¯a,¯b,¯c is [¯a,¯b,¯c]. Hence find the volume of the parallelopiped with coterminal edges ˆi+ˆj,ˆj+ˆkandˆk+ˆi.
Let the coterminal edges of a parallelopiped are →a,→b,and→c respectively.
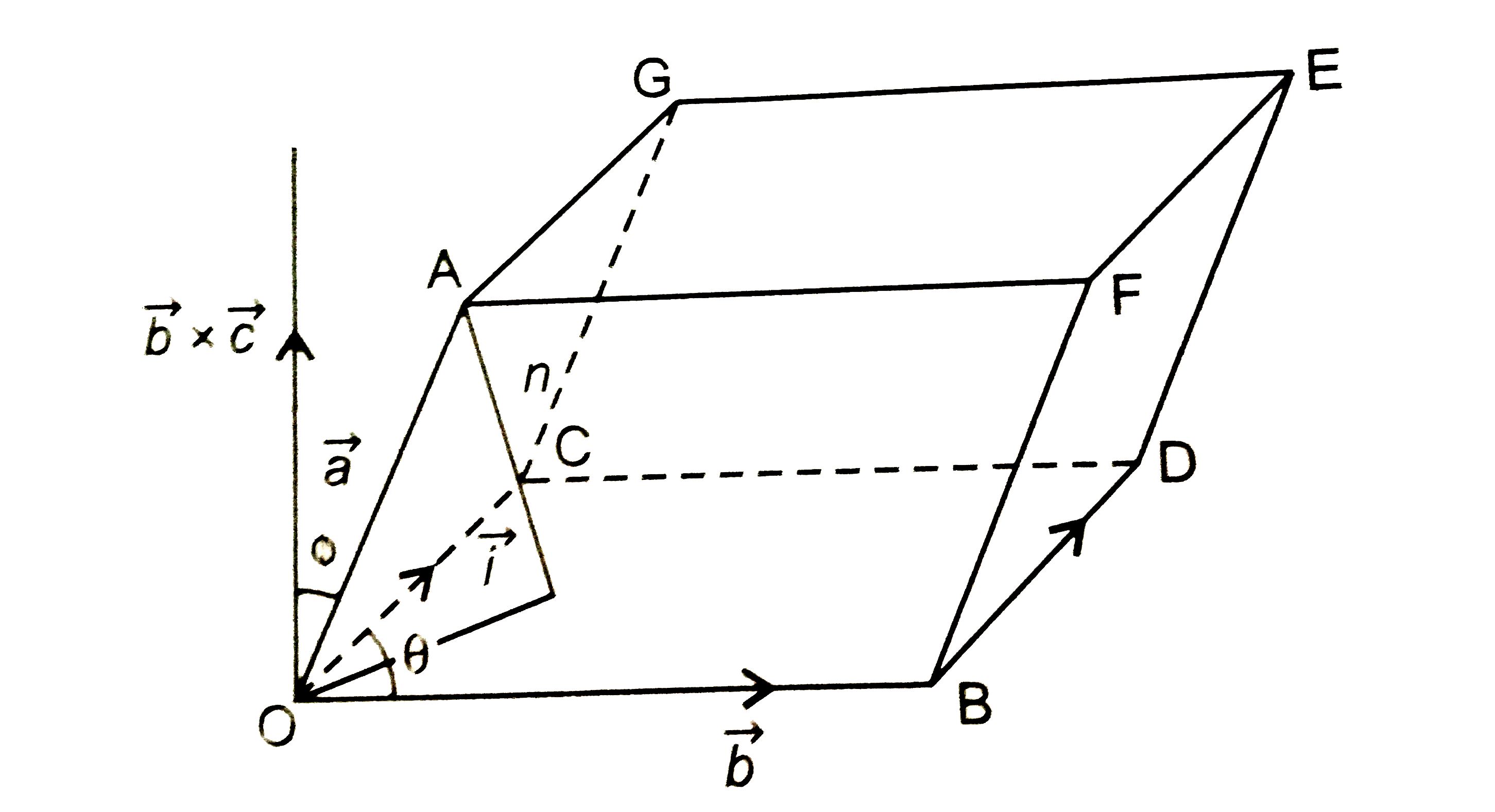
→n=→b×→c=∣∣→b×→c∣∣ˆn
= (Area of parallelogram OBDC) ˆn
=∣∣→b∣∣|→c|sinθˆn
Then →a⋅(→b×→c)=|→a|∣∣→b×→c∣∣cosϕ
=|→a|∣∣→b∣∣|→c|sinθcosϕ
=∣∣→b∣∣|→c|sinθsinθ.|→a|cosϕ
= (Area of parallelogram OBDC)x (Height of side OA)
[→a→b→c]= Volume of parallelopiped
Given, →a=ˆi+ˆJ,
→b=ˆJ+ˆk
→c=ˆk+ˆi
V=[→a→b→c]=∣∣
∣∣110011101∣∣
∣∣
=1(1−0)−1(0−1)+0
=1+1
= 2 unit
Topper's Solved these Questions
Similar Questions
If y=sec−1(√x−1x+√x)+sin−1(x+√x√x−1), then dydx= ……………
View SolutionIf X is the a random variable with probability mass function P(x)=kx, for x = 1,2,3
= 0 , otherwise
then k = ……..
View SolutionIf ¯a=3ˆi−2ˆj+7ˆk,¯b=5ˆi+ˆj−2ˆkand¯c=ˆi+ˆj−ˆk, then find ¯a⋅(¯bׯc).
View SolutionFind the volume of the parallelopiped whose cotermius edges are 2ˆi+ˆj+3ˆk,−ˆi+2ˆj+ˆkand3ˆi+ˆj+2ˆk.
View SolutionLet ¯a=2¯i+¯j−3¯kand¯b=¯i+3¯j+2¯k. then the volume of the parallelopiped having coterminous edge as ¯a,¯band¯c,where¯c is the vector perpendicular to the plane of ¯a,¯b|¯c|=2 is
View SolutionIf the volume of the tetrahedron formed by the coterminous edges ¯a,¯band¯c is 4, then the volume of the parallelopiped formed by the coterminous edges ¯aׯb,¯bׯcand¯cׯa is
View SolutionIf OA=6ˆi+3ˆj−4ˆk,OB=2ˆj+ˆk,OC=5ˆi−ˆj+2ˆk are the coterminous edges of a parallelopiped, then the height of the parallelopiped drawn from the vertex A is
View SolutionFind the volume of a parallelopiped with coterminous edges represented by the vectors 3ˆi+4ˆj,2ˆi+3ˆj+4ˆk and 5ˆk.
View SolutionThe volume (in cubic units) of the parallelopiped whose edges are represented by the vectors ˆi+ˆj,ˆj+ˆk and ˆk+ˆi is
View SolutionFind the volume of the parallelepiped whose coterminous edges are represented by the vector: →a=2ˆi+3ˆj+4ˆk, →b=ˆi+2ˆj−ˆk, →c=3ˆi−ˆj+2ˆk .
View SolutionFind the volume of the parallelepiped whose coterminous edges are represented by the vector: →a=2ˆi−3ˆj+4ˆk, →b=ˆi+2ˆj−ˆk, →c=3ˆi−ˆj−2ˆk .
View SolutionFind the volume of the parallelepiped whose coterminous edges are represented by the vector: →a=ˆi+ˆj+ˆk, →b=ˆi−ˆj+ˆk, →c=ˆi+2ˆj−ˆk .
View SolutionThe volume of parallelopiped with vectors ¯a+2¯b−¯c,¯a−¯b,¯a−¯b−¯c as coterminous edges is K[¯a¯b¯c] then |K| =
View SolutionIf V is the volume of the parallelopiped having three coterminous edge, as, ¯a,¯b and ¯c then the volume of the parallopiped having three coterminous edges as
¯¯¯α=(¯a.¯a)¯a+(¯a.¯b)¯b+(¯a.¯c)¯c
¯β=(¯b.¯a)¯a+(¯b.¯b)¯b+(¯b.¯c)¯c
¯γ=(¯c.¯a)¯a+(¯c.¯b)¯b+(¯c.¯c)¯c is
View SolutionIf the vectors 2ˆi−3ˆj,ˆi+ˆj−ˆk and 3ˆi−ˆk form three concurrent edges of a parallelopiped, then find the volume of the parallelopiped.
View Solution
