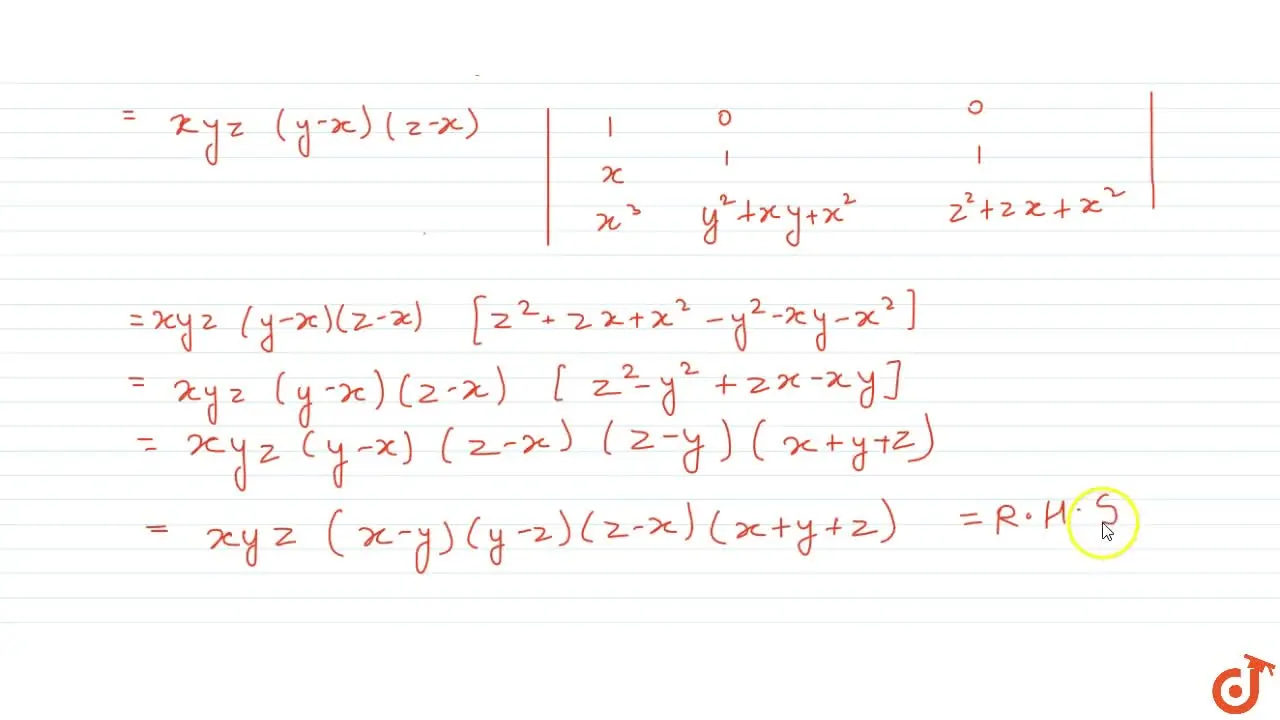Prove the identities: ∣∣ ∣ ∣∣zxyz2x2y2z4x4y4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xyzx2y2z2x4y4z4∣∣ ∣ ∣∣=∣∣ ∣ ∣∣x2y2z2x4y4z4xyz∣∣ ∣ ∣∣ =x y z (x-y)(y-z)(z-x)(x+y+z)
Video Solution
Text Solution
$$\left|\begin{array}{ccc}z & x & y \\ z^{2} & x^{2} & y^{2} \\ z^{4} & x^{4} & z^{4}\end{array}\right|=\left|\begin{array}{ccc}x & y & z \\ x^{2} & y^{2} & z^{2} \\ x^{4} & y^{4} & z^{4}\end{array}\right|=\left|\begin{array}{ccc}x^{2} & y^{2} & z^{2} \\ x^{4} & y^{4} & z^{4} \\ x & y & z\end{array}\right|$$ $$=x y z(x-y)(y-z)(z-x)(x+y+z)$$ $$\left|\begin{array}{ccc}x & y & z \\ x^{2} & y^{2} & z^{2} \\ x^{4} & y^{4} & z^{4}\end{array}\right|$$ $$=x y z\left|\begin{array}{ccc}1 & 1 & 1 \\ x & y & z \\ x^{3} & y^{3} & z^{3}\end{array}\right|$$ $$=x y z\left|\begin{array}{ccc}0 & 1 & 0 \\ x-y & y & z-y \\ x^{3}-y^{3} & y^{3} & z^{3}-y^{3}\end{array}\right|$$ $$=x y z(x-y)(z-y)\left|\begin{array}{ccc}0 & 1 & 0 \\ 1 & y & 1 \\ x^{2}+y^{2}+x y & y^{3} & z^{2}+y^{2}+z y\end{array}\right|$$ $$=-x y z(x-y)(z-y)\left[z^{2}+y^{2}+z y-x^{2}-y^{2}-x y\right]$$ $$=-x y z(x-y)(z-y)[(z-x)(z+x)+y(z-x)]$$ $$=-x y z(x-y)(z-y)(z-x)(x+y+z)$$ = R.H.S
|
Updated on:21/07/2023
Related Playlists
Similar Questions
Prove that ∣∣ ∣ ∣∣xx2x4yy2y4zz2z4∣∣ ∣ ∣∣=xyz(x−y)(y−z)(z−x)(x+y+z)
View SolutionIf x+y=2z then xx−z+zy−z=?
View Solution∣∣ ∣ ∣∣y+zxxyz+xyzzx+y∣∣ ∣ ∣∣= (i) x2y2z2 (ii) 4x2y2z2 (iii) xyz (iv) 4xyz
View Solution(4x−2y+z)(5x−5y+z)
View SolutionShow that : ∣∣xyzx2y2z2x3y3z3∣∣=xyz(x−y)(y−z)(z−x).
View SolutionProve that Det⎡⎢⎣x+y+2zxyzy+z+2xyzxz+x+2y⎤⎥⎦=2(x+y+z)3
View SolutionShow that ∣∣ ∣ ∣∣y+zxxyz+xyzzx+y∣∣ ∣ ∣∣=4xyz
View Solution2x=3y=4z,x:y:z
View SolutionProve the following :
∣∣ ∣ ∣∣xyzx2y2z2x3y3z3∣∣ ∣ ∣∣=∣∣ ∣ ∣∣xx2x3yy2y3zz2z3∣∣ ∣ ∣∣=xyz(x−y)(y−z)(z−x)View Solution8 x+y + 2z =4 x+2y + z =1 x+y+z = 2
View Solution