Pyramid a pyramid is a solid whose base is a plane rectilinear figure and whose side-faces are triangles having a common vertex outside the plane of the base.
Pyramid
A pyramid is a 3-dimensional geometrical figure with a base (any polygon), and three or more triangular sides that meet at a point called the apex. These triangular faces are sometimes called the lateral faces to differentiate them from the base.
Types of Pyramids
There are different types of pyramids, depending on the shapes of their bases.
- Triangular Pyramid
- Square Pyramid
- Pentagonal Pyramid
- Right Pyramid
- Oblique Pyramid
Triangular Pyramid
The base of this pyramid is triangular.
Square Pyramid
As the name suggests, the base of this pyramid has a square shape.
Pentagonal Pyramid
This pyramid has a base of a pentagon shape; therefore, we call it a Pentagonal Pyramid.
Right Pyramid
The apex or pinnacle point of this pyramid is exactly over the centre point of the base.
Oblique Pyramid
The apex or pinnacle point of this pyramid is not exactly over the centre point its base.
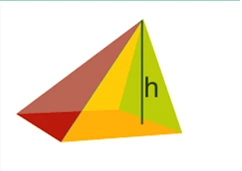
Pyramid Formulae
The pyramid surface area is the total area of all the faces plus base area, including perimeter and slant height,
Surface Area = (base area) + (1/2) × (perimeter) × (slant height)
To determine the volume of pyramid, the formula is;
Volume = 1/ 3 × (Base Area) × height
Base area is the area of the base of the pyramid, which will change based on its types.
Related Video:
Volume of Pyramid
The volume of a pyramid depends on the sort of pyramid's base, regardless of whether it is a triangle, square or square shape. The base of the pyramid is a polygon with 3 or more sides. Subsequently, the equation to discover volume, as well as the surface area of a pyramid, depends on the structure of its base and slant height.
Volume of Triangular Pyramid
Since this pyramid has a triangular base.
The area of a triangle;
A = 1/2 base (b) x height (h)
Thus, the volume of a triangular pyramid is,
= 1/3 x Area of base (traingle) x Height of pyramid (H)
V = 1/3 x (1/2 b.h) x H
Volume of Triangular Pyramid = 1 /6 b.h.H
Volume of Square Pyramid
This pyramid has a square shape base.
Since, the area of a square is:
A = s2
Where s is the length of the side of the square.
Thus, the volume of a square pyramid is given by:
Volume = 1/3 x Area of base (square) x Pyramid Height (H)
V = 1/3 x s2 x H
Volume of Square Pyramid = 1/3 . s2 . H
Volume of Rectangular Pyramid
This pyramid has a rectangular base.
Since, the area of rectangle :
A = Length x breadth
A = l x b
Thus, the volume of a rectangular pyramid will be:
V = 1/3 x A x Height of Pyramid (H)
Volume of Rectangular Pyramid = 1/3 l . b . H
Volume of Hexagonal Pyramid
This pyramid has a hexagonal base.
Volume of pyramid = 1/3 x area of base x pyramid height (H)
Area of hexagonal base = 3√3/2 a2 , a is length of each side of a hexagon
Volume of Hexagonal pyramid = 1/3 x 3√3/2 a2 x H
Volume of Hexagonal pyramid = √3/2 a2 H
Solved Questions
Q1. Find the volume of a square pyramid. Given, the sides of the base are 20 cm each and the height of the pyramid is 15cm.
Sol: Volume of a pyramid, V = ⅓ A H
The area of the square base is a2 = 20 x 20 = 400 cm2
Thus,
Volume of Square pyramid= ⅓ x 400 cm 2 x 15 cm
= 400 x 5
V= 2000 cm3
Q 2. Find the volume of a square pyramid. Given, the sides of the base are 10 cm each and the height of the pyramid is 12cm.
Sol: Volume of a pyramid, V = ⅓ A H
The area of the square base is a2 = 10 x 10 = 100 cm2
Thus,
Volume of Square pyramid = ⅓ x 100 cm 2 x 12 cm
= 100 x 4
V= 400 cm3
Q 3. . Find the volume of a rectangular pyramid having base length 5 cm and the breadth is 8 cm and the height of the pyramid is 15cm.
Sol: Length of rectangular base of pyramid = 5 cm
Breadth of rectangular base of pyramid = 8 cm
and height of the pyramid = 15 cm
Volume of rectangular pyramid,
V = 1/3 l .b . H
On putting the respective values we get;
V = 1/3 x 5 x 8 x 15
V = 600/3
V= 200 cm3
Q 4: The area of the base of a triangular pyramid is 150 cm2 and the height of the pyramid is 6 cm. Find the volume of the pyramid
Sol: Area of the base of pyramid = 150 cm2
Volume of Pyramid = 1/3 x A x H
V = 1/3 x 150 x 6
V = 900/3
Volume of the triangular pyramid = 300 cm3
Q5. Find the volume of a square pyramid. Given, the sides of the base are 10 cm each and the height of the pyramid is 12cm.
Sol: Volume of a pyramid, V = ⅓ A H
The area of the square base is a2 = 10 x 10 = 100 cm2
Thus,
Volume of Square pyramid= ⅓ x 100 cm 2 x 12 cm
= 100 x 4
Volume of square pyramid = 400 cm3
Q6. Find the volume of a triangular pyramid. Given, the area of base is 125 cm2 , and height and the height of the pyramid is 12cm.
Sol: Area of the base of triangular pyramid = 115 cm2
Volume of Pyramid = 1/3 x A x H
V = 1/3 x 125 x 12
V = 125 x 4
Volume of a triangular pyramid = 500 cm3
Q 7. Find the volume of a rectangular pyramid having base length 10 cm and the breadth is 6 cm and the height of the pyramid is 12 cm.
Sol: Length of rectangular base of pyramid = 10 cm
Breadth of rectangular base of pyramid = 6 cm
and height of the pyramid = 12 cm
Volume of rectangular pyramid,
V = 1/3 l .b . H
On putting the respective values we get;
V = 1/3 x 10 x 6 x 12
V = 10x 6 x 4
V= 240 cm3
Important Chapters:





Similar Questions
Knowledge Check
A pyramid is a solid figure whose base is
Aonly a triangleBonly a squareConly a rectangleDany polygonA pyramid is a polyhedron whose lateral faces are
ARectanglesBTrianglesCParallelogramsDRhombuses or RhombiA pyramid is a solids figure, the base of which is
Aonly a triangleBonley a squareConly a rectangleDany polygon
Regular pyramid a pyramid is said to be a regular pyramid if its base is a regular figure.
View SolutionHaving given the bases and the sum of the areas of a number of triangles which have a common vertex, show that the locus of the vertex is a straight line.
View SolutionRegular pyramid a pyramid is said to be a regular pyramid if its base is a regular figure i.e. all sides of its base are equal.
View SolutionFind the number of vertices of a pyramid, whose base is a pentagon.
View SolutionRight pyramid a pyramid is said to right pyramid if the perpendicular dropped from the vertex on the base meets the base at its central point i.e. the centre of the inscribed or circumscribed circle. In other words the vertex of the pyramid lies on the perpendicular to the base drawn through its centre. Otherwise the pyramid is called an oblique prism.
View Solution
