Red tides is a form of harmful algae that release toxins as it breaks down in the environment. A marine biologist is testing a new spray, composed of clay and water, hoping to kill the red tide that almost completely covers a beach in southern Floride. He applies the spray to a representative sample of 200 square feet of the beach. By thhe end of the week, 184 square feet of the beach is free of the red tide. Based on these results, and assuming the same general conditions, how much of the 10,000-squarefoot beach would still be covered by red tide if the spray had been used on the entire area?
800 sq ft
920 sq ft
8,000 sq ft
9,200 sq ft
The correct Answer is:A
To solve the problem step by step, we can follow these calculations:
Step 1: Calculate the percentage of the area that is free of red tide.
The marine biologist applied the spray to a sample area of 200 square feet, and by the end of the week, 184 square feet was free of red tide.
Percentage of area free of red tide=(184200)×100
Step 2: Perform the calculation.
Calculating the percentage:
184200=0.92
Now, converting to percentage:
0.92×100=92%
Step 3: Calculate the area free of red tide on the entire beach.
Now, we need to apply this percentage to the entire beach area of 10,000 square feet.
Area free of red tide=92% of 10,000=(92100)×10,000
Step 4: Perform the calculation.
Calculating the area:
(92100)×10,000=9200 square feet
Step 5: Calculate the area still covered by red tide.
To find out how much of the beach is still covered by red tide, we subtract the area that is free from red tide from the total area of the beach.
Area still covered by red tide=10,000−9200
Step 6: Perform the calculation.
Calculating the area still covered:
10,000−9200=800 square feet
Final Answer:
The area still covered by red tide is 800 square feet.
---
The marine biologist applied the spray to a sample area of 200 square feet, and by the end of the week, 184 square feet was free of red tide.
Calculating the percentage:
Now, we need to apply this percentage to the entire beach area of 10,000 square feet.
Calculating the area:
To find out how much of the beach is still covered by red tide, we subtract the area that is free from red tide from the total area of the beach.
Calculating the area still covered:
The area still covered by red tide is 800 square feet.
Topper's Solved these Questions
Similar Questions
Knowledge Check
What is the area, in square feet, of the figure below?
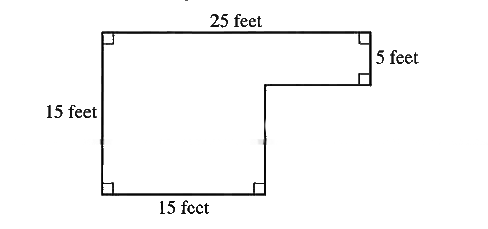 A60B80C275D375
A60B80C275D375The top surface of a rectangular table has an area of 100 square feet and a width of 5 feet. What is the length, in feet, of the surface?
A10B15C20D95
Spraying kerosene on stagnant water shall kill Anopheles due to
View SolutionOrganisms responsible for red tides in seas.
View SolutionRed oceanic tides can be due to
View SolutionWhat is the minimum possible perimeter of a quadrilateral with an area of 1,600 square feet?
View SolutionA landscape is designing a rectangular garden. The length of the garden is to be 5 feet longer than the width. IF the area of the garden will be 104 square feel, what will be the length in feet, of the garden?
View SolutionWhy are red tides caused and why are they harmful ?
View Solution
