Refer to the figure for the problem below in which AT and BT are tangent from T to circle centre O.
(a) If AˆTB=65∘, find AˆOT
(b) If AˆTB=64∘, find AˆOB
( c ) If AˆTB=40∘, find T hat A B
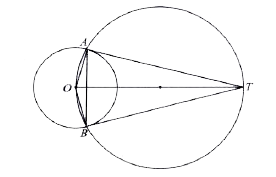
The correct Answer is:5712∘ (b)116∘ (c)70∘
Topper's Solved these Questions
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - TEST YOURSELF (LEVEL 2)
4 Videos
- TANGENTS TO CIRCLES BOOK - CENGAGECHAPTER - TANGENTS TO CIRCLES EXERCISE - TEST YOURSELF (LEVEL 3)
32 Videos
- STANDARD AND ALLIED ANGLESBOOK - CENGAGECHAPTER - STANDARD AND ALLIED ANGLESEXERCISE - Olympiad And NTSE Level Exercises
10 Videos
- TRANSFORMATIONSBOOK - CENGAGECHAPTER - TRANSFORMATIONSEXERCISE - Olympiad and NTSE level exercises
10 Videos
Similar Questions
If →a=3ˆi−ˆj+2ˆk and →b=2ˆi+ˆj−ˆk then find(→a×→b)→a.
View SolutionIf →a=3ˆi−ˆj+2ˆk and →b=2ˆi+ˆj−ˆk then find(→a×→b)→a.
View SolutionIn Figure, ˆAB≅ˆAC and O is the centre of the circle. Prove that OA is the perpendicular bisector of BC
View SolutionFind the area of the triangle formed by O,A,B when →OA=ˆi+2ˆj+3ˆk,→OB=−3ˆi−2ˆj+ˆk.
View SolutionFind the area of the triangle formed by O,A,B when →OA=ˆi+2ˆj+3ˆk,→OB=−3ˆi−2ˆj+ˆk.
View SolutionIf →a=(ˆi+ˆj+ˆk),→a.→b=1and→a×→b=ˆj−ˆk,thenˆb is ˆi−ˆj+ˆk b. 2ˆj−ˆk c. ˆi d. 2ˆi
View SolutionIf →a=3ˆi−ˆj−4ˆk,→b=2ˆi+4ˆj−3ˆk and →c=ˆi+2ˆj−ˆk, find ∣∣3→a−2ˆb+4ˆc∣∣.
View SolutionA uni-modular tangent vector on the curve x=t2+2,y=4t−5,z=2t2−6t=2 is a. 13(2ˆi+2ˆj+ˆk) b. 13(ˆi−ˆj−ˆk) c. 16(2ˆi+ˆj+ˆk) d. 23(ˆi+ˆj+ˆk)
View SolutionLet g(θ)=∫∣∣ˆa׈b∣∣2−(ˆa,ˆb)2(2t+1)dt, where θ is the angle between ˆaandˆb. If volume of the parallelopinea whose coterminous edges are represented by vectors ˆa,ˆa׈bandˆa×(ˆa׈b) (where angle between ˆaandˆb is taken from the equation 2g(θ)–1=0), is pq then find the least value of (p+q).
View SolutionLet →A(t)=f1(t)ˆi+f2(t)ˆjand→B(t)=g(t)ˆi+g2(t)ˆj,t∈[0,1],f1,f2,g1g2 are continuous functions. If →A(t)and→B(t) are non-zero vectors for all tand→A(0)=2ˆi+3ˆj,→A(1)=6ˆi+2ˆj,→B(0)=3ˆi+2ˆiand→B(1)=2ˆi+6ˆj Then,show that →A(t)and→B(t) are parallel for some t.
View Solution
