Seg AM is a median of ΔABC, if AB = 22, AC = 34, BC = 24, find AM.Solution in Tamil
The correct Answer is:AM = 26 units
Step by step video, text & image solution for Seg AM is a median of Delta ABC, if AB = 22, AC = 34, BC = 24, find AM. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- PYTHAGORAS THEOREMBOOK - CHETAN PUBLICATIONCHAPTER - PYTHAGORAS THEOREMEXERCISE - Problem Set - 2 (MCQ)
8 Videos
- PYTHAGORAS THEOREMBOOK - CHETAN PUBLICATIONCHAPTER - PYTHAGORAS THEOREMEXERCISE - Additional MCQ.s
10 Videos
- PYTHAGORAS THEOREMBOOK - CHETAN PUBLICATIONCHAPTER - PYTHAGORAS THEOREMEXERCISE - Practive Set - 2.2
1 Videos
- MODEL ACTIVITY SHEET BOOK - CHETAN PUBLICATIONCHAPTER - MODEL ACTIVITY SHEET EXERCISE - QUESTION
29 Videos
- QUADRATIC EQUATIONSBOOK - CHETAN PUBLICATIONCHAPTER - QUADRATIC EQUATIONSEXERCISE - ASSIGNMENT
12 Videos
Similar Questions
Out of the following which is the pythagorean triplet?
View SolutionIn ΔRST,∠s=90∘,RT=12m,ST=8 m then RS=
View SolutionIn ΔABC,AB=10,AC=7,BC=9 find the length of the median drawn from C to side . AB. Given
(i) In ΔABC,seg CMis a median(ii)AB=10,AC=7BC=9

View SolutionWhat is the ratio of 1mm 1cm ?
View SolutionIf α and β are the roots of quadratic equation 2x2+4x+3=0, then the value of α+β=
View SolutionAM is a median of s triangle ABC. Is AB+BC+CA>2AM? (Consider the sides of triangles ΔABMandΔAMC.
View SolutionIf in ΔABC, seg AM is the median, AB2+AC2=410 and BC=12 then AM=?
View SolutionIn ΔABC, seg AP is a median. If BC = 18, AB2+AC2=260 then find the length of AP.
View SolutionSeg AM is a median of ΔABC. If AB =22, AC =34, BC = 24, find AM.
View SolutionIn ΔABC,segAPis a median.IfBC=18,AB2+AC2=260findAP.
View SolutionAM is a median of s triangle ABC. Is AB+BC+CA>2AM? (Consider the sides of triangles ΔABMandΔAMC.
View SolutionIn ΔABC, ∠ABC=90∘, BM⊥AC, AM=8x2,AM=2x2, find BM and AB.

View SolutionIn fig., AD is a median of a triangle ABC and AM ⊥ BC.Prove that :- AC2=AD2+BC.DM+(BC2)2 .
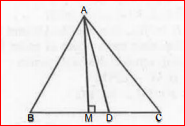 .
.
View SolutionIn fig., AD is a median of a triangle ABC and AM ⊥ BC.Prove that :- AB2=AD2−BC.DM+(BC2)2 .
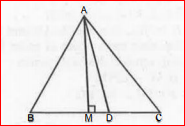 .
.
View SolutionIn △ABC, point M is midpoint of side BC. If AB2+AC2=290cm2 and AM=8 cm, find BC.
View Solution
