Select the correct option.
The 15th term from the end in the A.P. 13, 16, 19, ..., 160 is 108.
If the first, second and last terms of an A.P. are 6, 9 and 33 respectively, then the number of terms of the A.P. is 10.
The sum of an A.P. 2, 5, 8, ...., 152 is 3925.
All of these
The correct Answer is:B
To solve the problem step by step, we need to analyze the given arithmetic progression (AP) and find the correct option based on the information provided.
1. Identify the AP: The given arithmetic progression is:
13,16,19,…,160
Here, the first term a=13 and the common difference d=16−13=3.
2. Find the number of terms: To find the number of terms in the AP, we can use the formula for the nth term of an AP:
an=a+(n−1)d
We need to find n such that an=160:
160=13+(n−1)⋅3
Rearranging gives:
160−13=(n−1)⋅3⟹147=(n−1)⋅3
Dividing both sides by 3:
n−1=49⟹n=50
3. Find the 15th term from the end: The 15th term from the end can be found using:
an−14=a+(n−14−1)d
Substituting n=50:
a50−14=a+(50−14−1)d=a+35d
Now substituting the values of a and d:
a36=13+35⋅3=13+105=118
4. Check the options: We have calculated the 15th term from the end to be 118. Now we need to check the options provided in the question to see if this matches any of them.
5. Conclusion: After checking the options, we find that the second option is correct as it states that the number of terms in the AP is 50, which we have calculated.
Final Answer:
The correct option is Option 2.
13,16,19,…,160
Here, the first term a=13 and the common difference d=16−13=3.
an=a+(n−1)d
We need to find n such that an=160:
160=13+(n−1)⋅3
Rearranging gives:
160−13=(n−1)⋅3⟹147=(n−1)⋅3
Dividing both sides by 3:
n−1=49⟹n=50
an−14=a+(n−14−1)d
Substituting n=50:
a50−14=a+(50−14−1)d=a+35d
Now substituting the values of a and d:
a36=13+35⋅3=13+105=118
The correct option is Option 2.
Topper's Solved these Questions
- IMO QUESTION PAPER 2019 SET BBOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET BEXERCISE - EVERYDAY MATHEMATICS
10 Videos
- IMO QUESTION PAPER 2019 SET ABOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2019 SET AEXERCISE - Achievers section
5 Videos
- IMO QUESTION PAPER 2020 SET 1BOOK - SCIENCE OLYMPIAD FOUNDATION CHAPTER - IMO QUESTION PAPER 2020 SET 1EXERCISE - Achievers Section
5 Videos
Knowledge Check
Selected the correct option :
A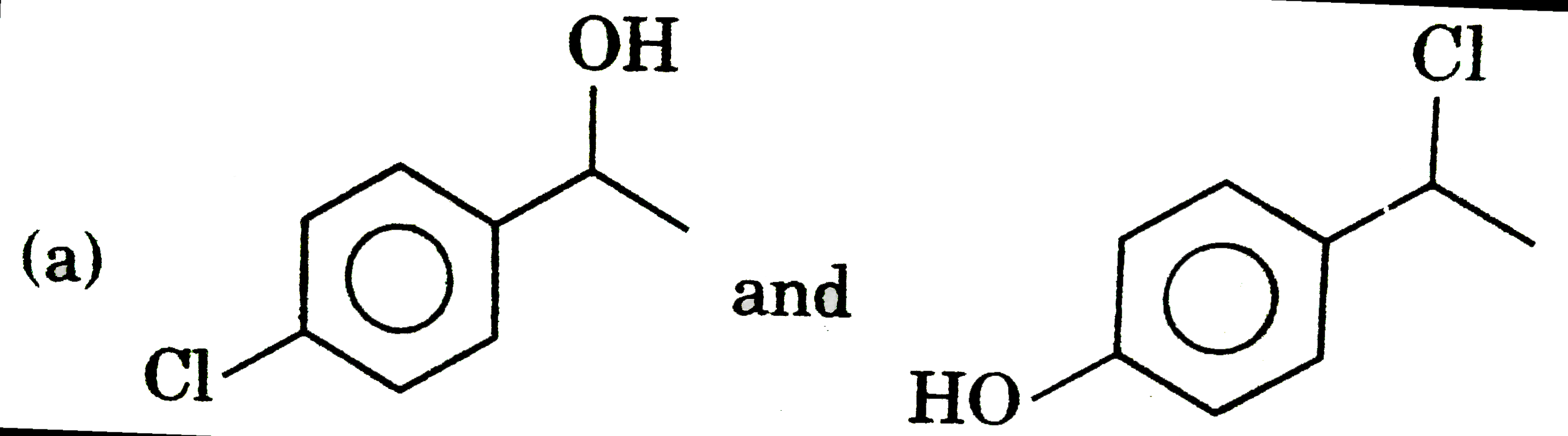
can be differentiated by Victor Meyer's test.B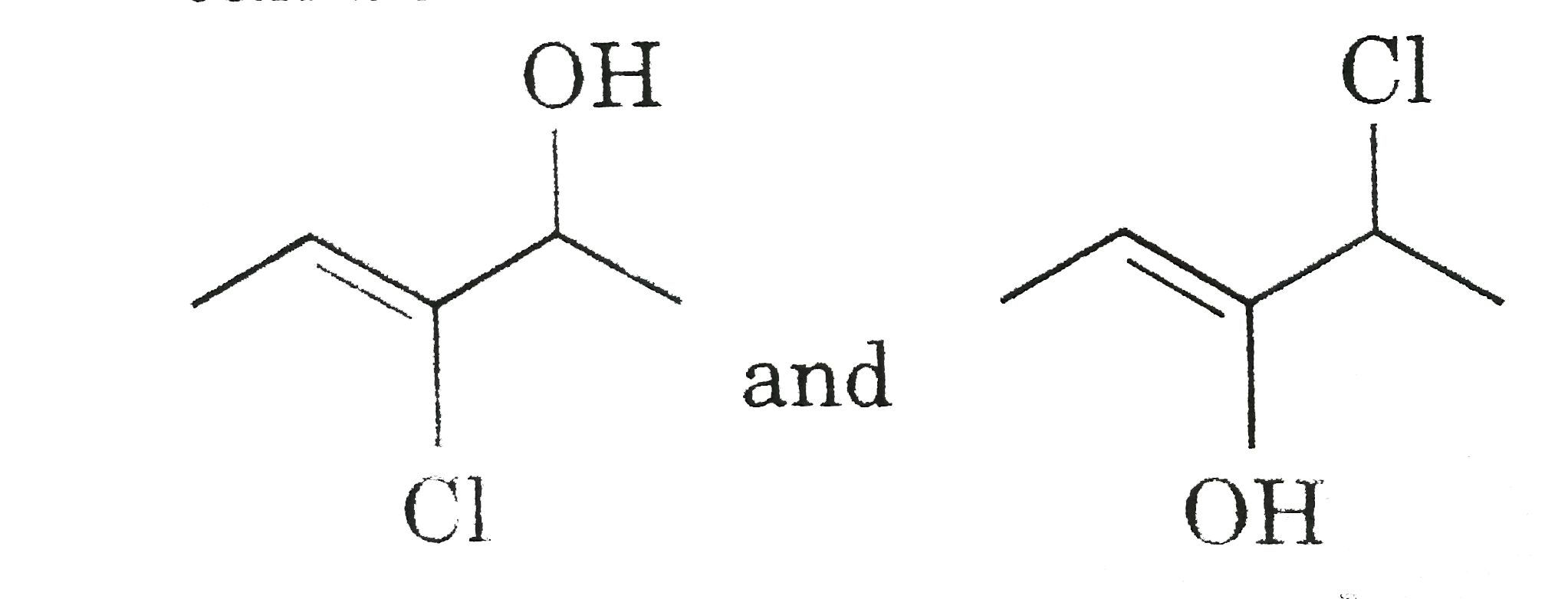 can be differentiated by Bielstien test.C
can be differentiated by Bielstien test.C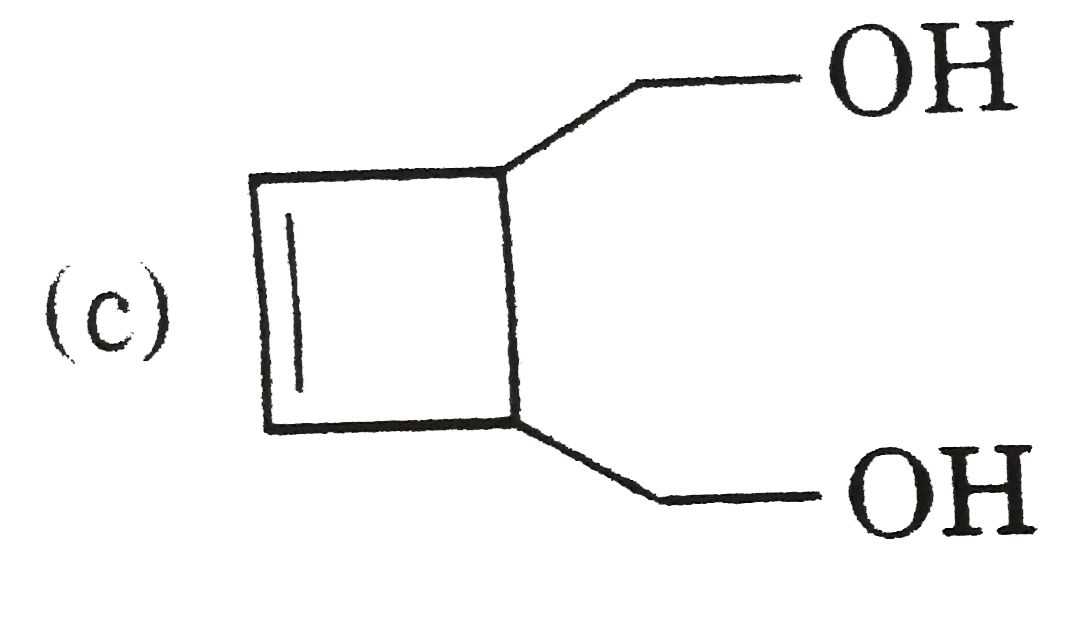
give purple colour with FeCl3Dwith NaOI Me−O∣∣C−O∣∣C−H gives sodium oxalate.Selected the correct option
AGenes are located on DNA and proteinBGene is the functional unit of inheritanceCA segment of DNA coding for a polypeptide is called a cistronDBoth (2) and (3)
