Shade the feasible region for the inequations 2x+3y≤6,x≥0,y≥0 in a rough figure. Solution in Odia
Step by step video & image solution for Shade the feasible region for the inequations 2x+3yle6,xge0,yge0 in a rough figure. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - PRACTICE QUESTIONS (Exams., Textbook.s & Other Imp. Questions) (4 Marks Questions)9videos
LINEAR PROGRAMMING
- BOOK - ARIHANT PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - PRACTICE QUESTIONS (Exams., Textbook.s & Other Imp. Questions) (6 Marks Questions)10videos
LINEAR PROGRAMMING
- BOOK - ARIHANT PRAKASHANCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test (6 MARKS Questions)3videos
INVERSE TRIGONOMETRIC FUNCTIONS
- BOOK - ARIHANT PRAKASHANCHAPTER - MATRICESEXERCISE - Chapter Test ( 6 Mark Questions)4videos
MATRICES
Similar Questions
Two types of food X and Y re mixed to prepare a mixture is such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin X. These vitamines are avialalbe in 1kg of food as per table below. 1kg of food X costs Rs 16 and 1kg of food Y costs Rs 20. Formulate the L. P. P. so as to determine the least cost of the mixture containing the required amound of vitamins.
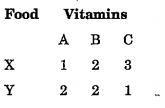 01:09View Solution
01:09View SolutionSolve the following LPP
Minimise Z=20x1+10x2
Subject to x1+2x2≤40
3x1+x2≥30
x1,x2≥0.02:39View SolutionIf sin−1(xa)+sin−1(yb)=αprove thatx2a2+2xyabcosα+y2b2=sin2α
View SolutionThere are two families A and B. There are 4 men, 6 women and 2 children in family A and 2 men, 2 women and 4 children in family B. The recommended daily amount of calories is 2400 for men, 1900 for women and 1800 for children, and 45 g of proteins for men, 55 g for women and 33 g for children. Represent the above information by matrices. Using matrices multiplication, calculate the total requirement of calories and proteins for each of the 2 families.
02:20View SolutionRegion represented by the inequalities x≥0,y≥0 is
07:56View SolutionThe vertex of the linear inequalities 2x+3y≤6,x+4y≤4,x≥0,y≥0 is
06:36View Solutionरेखीय असमिका 2x+3y≤6,x+4y≤4,x≥0,y≥0 के हल समुच्चय का ग्राफ खींचिए -
02:19View SolutionThe area of the feasible region for the following constraints 3y+x≥3,x≥0,y≥0 will be
09:32View Solution2x+3y≤6,x+4y≤4,x≥0,y≥0
02:42View SolutionConsider the linear inequalities
2x+3y≤6,2x+y≤4,x,y≥0
Mark the feasible region.06:54View SolutionThe area of the feasible region for the following constraints 3y+xge3,xge0,yge0 will be
06:31View SolutionSolve graphically:
2x+y≥4,x+y≤3,2x−3y≤6
x≥0,y≥002:56View SolutionFind the feasible region of the system. 2y−x≥0,6y−3x≤21,x≥0,y≥0
10:23View SolutionShade the feasible region satisfying ineuations x+2y≤10, x+y≥1, x−y<0 and x≥0,y≥0.
06:41View SolutionShade the feasible region satisfying ineuations 4x+3y≤60, 2x−y≤0, x−3≥0 and x≥0,y≥0.
04:26View SolutionFind the feasible region satisfying the inequation 2x+y≤4,x≥0,y≥0.
06:40View Solution

