Question

Show graphically that the system of equations
${\displaystyle 3x-y=2}$

${\displaystyle 9x-3y=6}$

has infinitely many solutions.

Explanation

(a) For equation 3x - y = 2
implies y = 3x - 2
`{:(x,-1,0,2),(y,-5,-2,4):}`
and for equation 9x - 3y = 6
implies 3y = 9x - 6
`y = (9x - 6)/(3)`
implies y = 3x - 2
`{:(x,-2,1,2),(y,-8,1,4):}`
Now, plot the points A(-1, -5), B(0, -2), C(2, 4) and P(-2, -8), Q(1, 1), R(2, 4) on the graph paper. We observe from the graph that two lines coincides. Hence, given system of equation has infinite number of solutions.
(b) For any two solutions,
Put x = 0 in equation (1), we get y = - 2
If we put x = 1 in the equation (1), we get y = 1 So, two solutions are `{:(x = 0),(y = - 2):}}` and `{:(x = 1),(y = 1):}}`

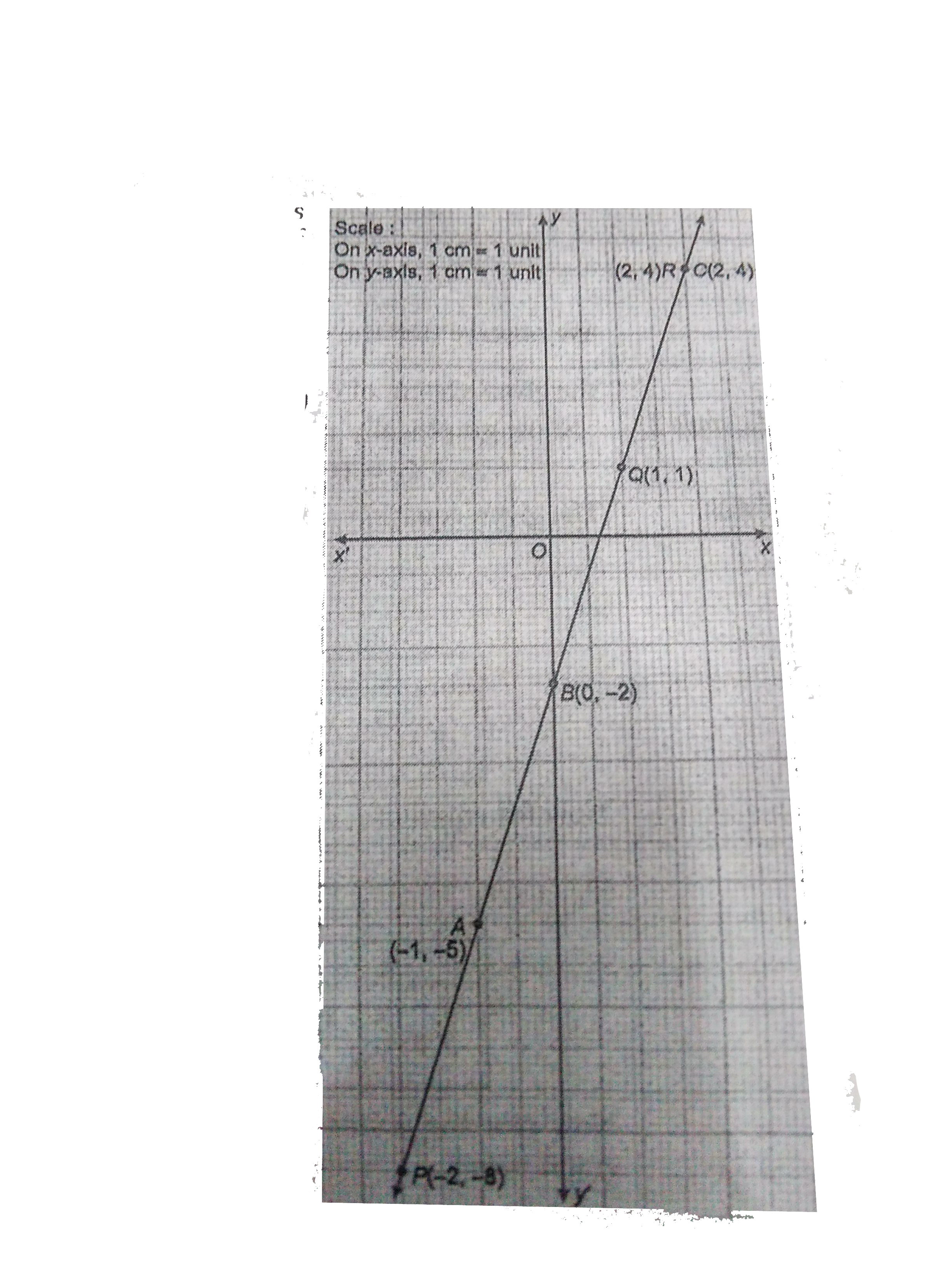
(c ) This line (both lines are same) cuts the y - axis at 2 units below the origin, So, its y - intercepts (part) is - 2.