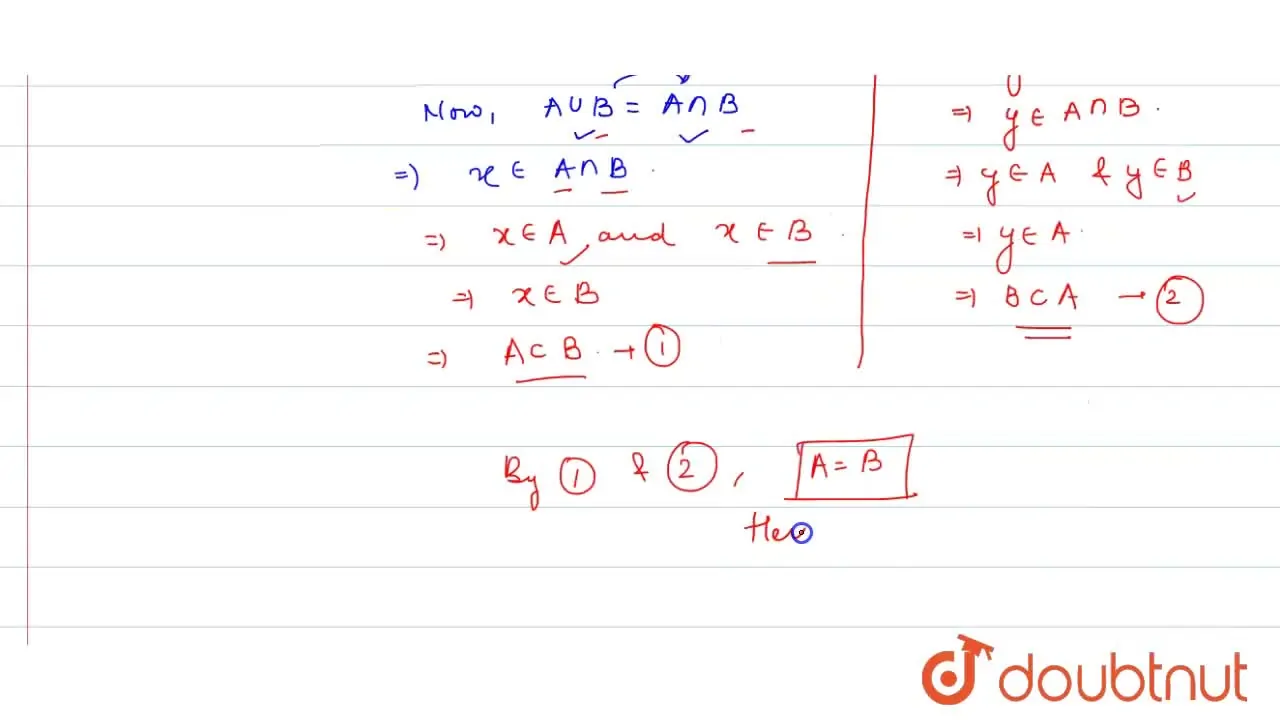
Show that A∩B=A∩Bimplies A=B
Video Solution
Text Solution
let a be an element
a∈A
then a∈(A∪B)
⇒a∈(A∩B) (given)
so, a∈B
if b∈B
then b∈(A∪B)
⇒b∈(A∩B)⇒b∈A
that means for all a∈A,a∈B&b∈B,b∈A
so, A=B
hence proved
|
Updated on:21/07/2023
Related Playlists
- BOOK - NCERTCHAPTER - SETSEXERCISE - MISCELLANEOUS EXERCISE3videos
SETS
- BOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.31videos
SETS
- BOOK - NCERTCHAPTER - SETSEXERCISE - EXERCISE 1.31videos
SETS
- BOOK - NCERTCHAPTER - RELATIONS AND FUNCTIONSEXERCISE - EXERCISE 1.314videos
RELATIONS AND FUNCTIONS
- BOOK - NCERTCHAPTER - THREE DIMENSIONAL GEOMETRYEXERCISE - QUESTION1videos
THREE DIMENSIONAL GEOMETRY
Similar Questions
Show that A∩B=A∩Bimplies A=B
View SolutionShow that A∩B=A∩C need not imply B=C
View SolutionIf A and B are any two sets, prove that
P(A) = P(B) implies A = B.View SolutionShow that A∩B=A∩C need not imply B=C.
View Solutiona.b=0 implies only
View SolutionShow that A∩B=A∩C need not imply B=C.
View SolutionLet A={(xy):X+y=p}, Be ={(x,y):x3+y3<p}
two sets sch that A∩B=ϕ for any real number p, than the exhastive intervals of p isView SolutionConsider the following relations:
1. A−B=A−(A∩B)
2. A=(A∩B)∪(A−B)
3. A−(B∪C)=(A−B)∪(A−C)
Which of these is/are correct ?View SolutionIf A and B ar two events such that P(A∪B)=56,P(A∩B)=13 and P(¯¯¯B=12) then the events A and B are
View SolutionIf A and B are two sets such that n(A)=7,n(B)=6and(A∩B)≠ϕ Then the greatest possible value of n (AΔB) is
View Solution