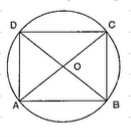
Show that if two chords of a circle bisect one another they must be diameters.
Video Solution
Text Solution
Given : AB and CD are two chords of a circle, intersecting at O such that OA = OB and OC=OD.
To Prove : AB and CD are diameters of the circle.
Construction : Join AC,AD and BC,BD
Proof : In ΔAOC and ΔBOD, we have
OA = OB [given]
OC = OD [given ]
∠AOC=∠BOD [ vert. opp. Δ]
∴ΔAOC≅ΔBOD
⇒AC=BD
⇒ˆAC=ˆBD ....(i)

In ΔAOD and ΔBOC, we have
OA=OB [ given]
OD=OC[given ]
∠AOD=∠BOC [ vert. opp. Δ]
∴DetlaAOD≅ΔBOC
⇒AD=BC ...(ii)
⇒ˆAD=ˆBC.
From (i) and (ii), we get
ˆAC+ˆAD=ˆBD+ˆBC
⇒ˆCAD=ˆCBD
⇒CD divided the circle into two semicircles
⇒ CD is a diameter.
Similarly , AB is a diameter.
|
Similar Questions
Knowledge Check
If AC and BD are two chords of a circle that bisect each other then quadrilateral ABCD is a
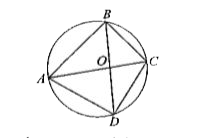 ArectangleBsquareCtrapeziumDparallelogram
ArectangleBsquareCtrapeziumDparallelogramIf two chords having lengths a2−1 and 3(a+1), where a is a constant of a circle bisect each other, then the radius of the circle is
A6B15/2C8D19/2
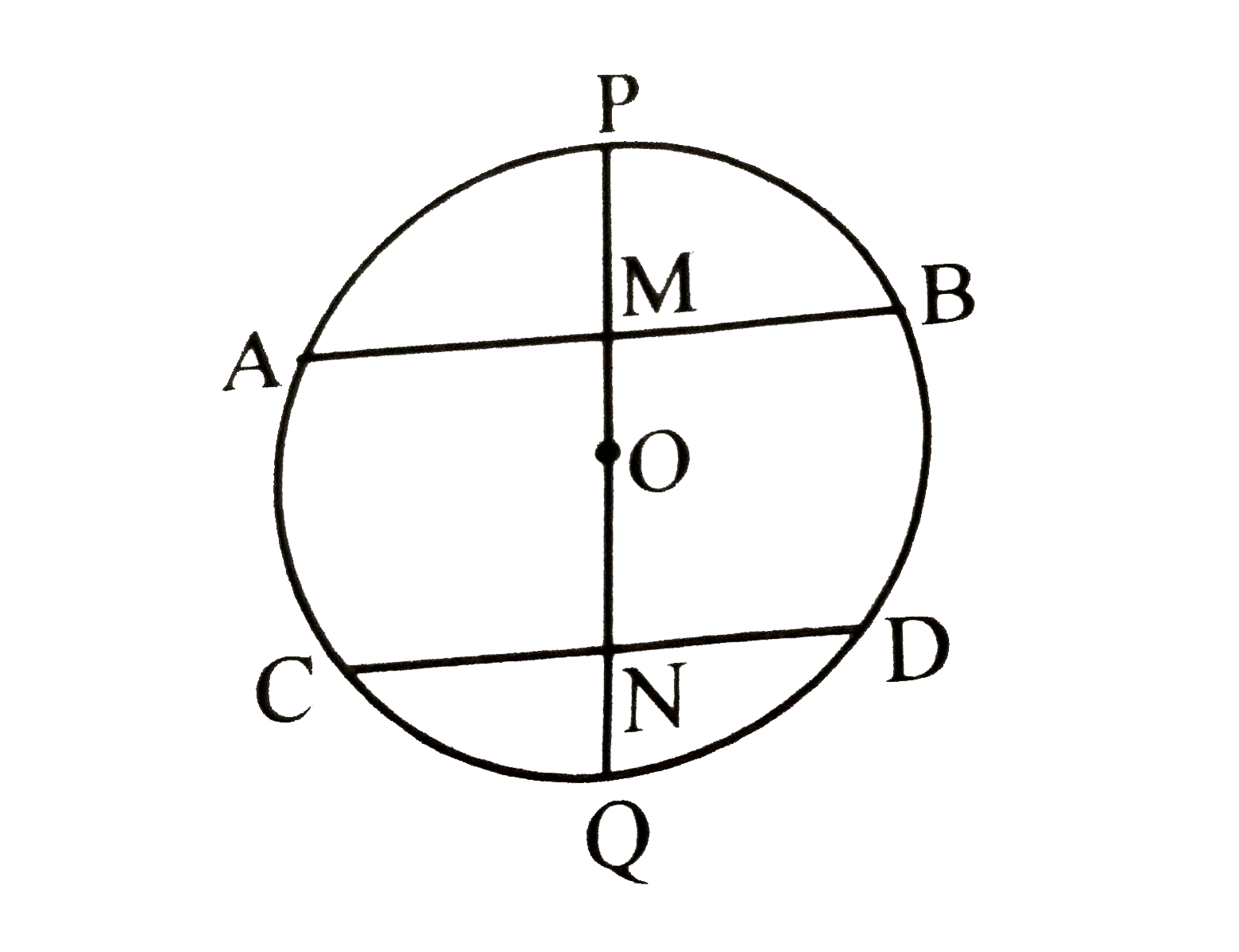
If a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionIf a diameter of a circle bisects each of the two chords of a circle, prove that the chords are parallel.
View SolutionProve that, if a diameter of a circle bisects two chords of the circle then those two chords are parallel to each other.
View SolutionIs every chord of a circle also a diameter?
View SolutionTwo equal circles intersect such that each passes through the centre of the other. If the length of the common chord of the circles is 10√3 cm, then what is the diameter of the circle?
View SolutionTheorem :-2 The perpendicular from centre of a circle to the chord bisects the chord and Perpendicular bisectors of two chords of a circle intersects at the centre.
View Solution