Show that limx→0e1/x−1e1/x+1 does not exist.Solution in Punjabi
Statement 1 is true, Statement 2 is true, Statement 2 is correct explanation for statement 1.
Statement 1 is true, Statement 2 is true, Statement 2 is not the correct explanation for statement 1.
Statement 1 is true, Statement 2 is false
Statement 1 is false, Statement 2 is true
The correct Answer is:B
Step by step video solution for Show that lim_(xto0)(e^(1//x)-1)/(e^(1//x)+1) does not exist. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - SOLVED EXAMPLES
1 Videos
- LIMITSBOOK - ARIHANT MATHSCHAPTER - LIMITSEXERCISE - Exercise (Single Option Correct Type Questions)
38 Videos
- INVERSE TRIGONOMETRIC FUNCTIONSBOOK - ARIHANT MATHSCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
8 Videos
- LOGARITHM AND THEIR PROPERTIESBOOK - ARIHANT MATHSCHAPTER - LOGARITHM AND THEIR PROPERTIESEXERCISE - Exercise (Questions Asked In Previous 13 Years Exam)
4 Videos
Similar Questions
To evaluate limx→a[f(x)], we must analyse the f(x) in right hand neighbourhood as well as in left hand neighbourhood of x=a. E.g. In case of continuous function, we may come across followign cases.
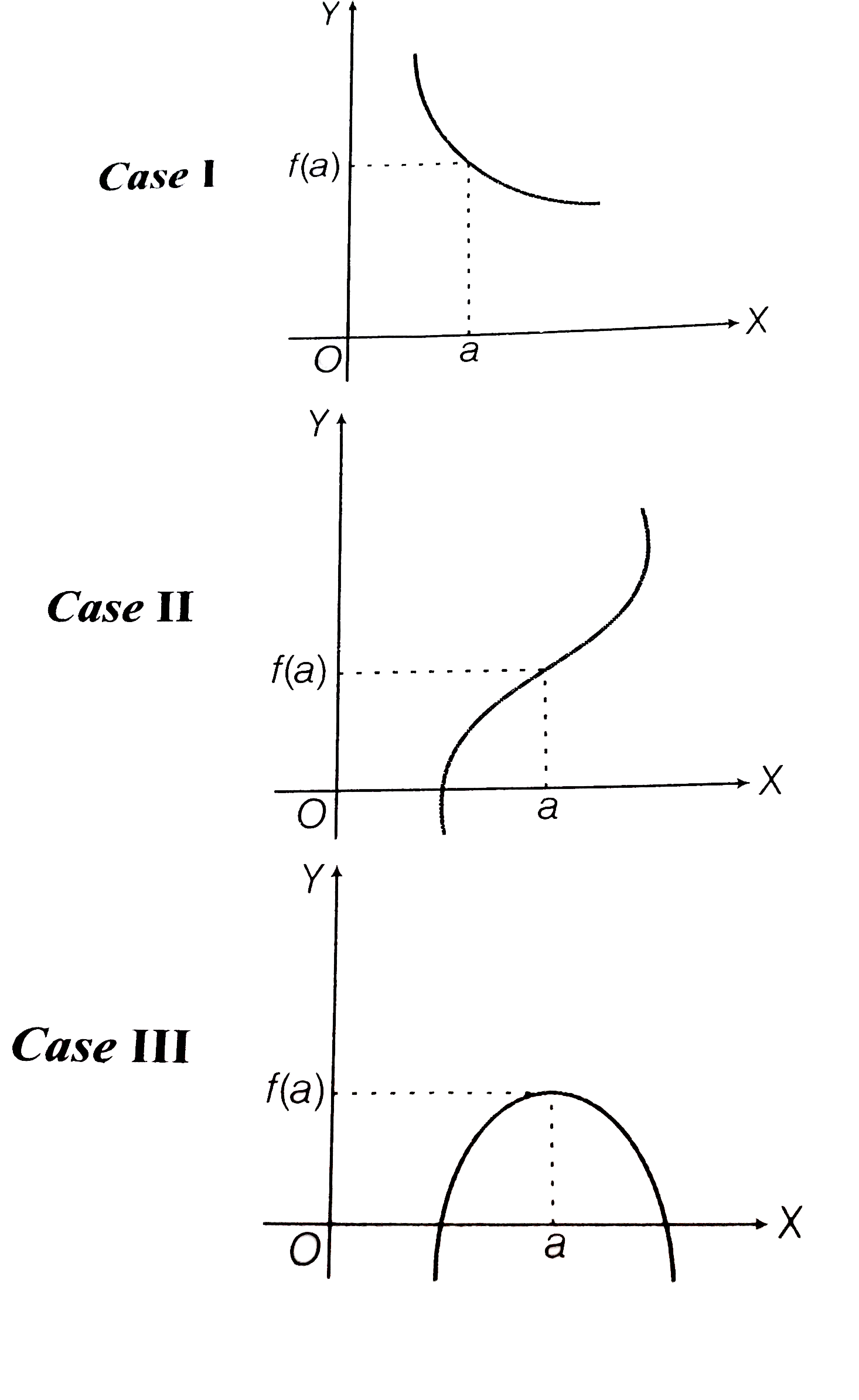

Iff(a) is an integer, the limit will exist in Case III and Case IV but not in Case I and Case II. If f(a) is not an integer, the limit exists in all the cases. ltbgt If f'(1)=−3 and limx→1[f(x)−12] does not exist, (where [.] denotes the greatest integer function), then
View Solutionlimx→0sin(πcos2(tan(sinx)))x2 is equal to
View SolutionIf α=3sin−1(611andβ=3cos−1(49), where the inverse trigonometric functions take only the principal values, then the correct options (s) is (are)
View SolutionIn Which quadrant Point (−2,−3) will be lie.
View SolutionFind the following limits: (i)limx→0(1−x)1x (ii)limx→1(1+logex)1logex
(iii)limx→0(1+sinx)1x
View SolutionConsider the following :
1. limx→01x exists.
2. limx→01ex does not exist.
Which of the above is/are correct?
View SolutionShow that limx→0−(e1/x−1e1/x+1) does not exist.
View SolutionShow that limx→0e−1/x does not exist.
View SolutionStatement 1: If limx→0{f(x)+sinxx} does not exist then limx→0f(x) does not exist.
Statement 2: limx→0(e1/x−1e1/x+1) does not exist.
View Solutionसिद्ध कीजिए कि limx→0e1/x−1e1/x+1 का अस्तित्व नहीं है।
View Solutionयदि f(x)=⎧⎨⎩e1/x1+e1/x,x≠00,x=0 तब limx→0f(x) का अस्तित्व ज्ञात कीजिए।
View Solutionlimx→0+(ex+x)1x
View SolutionShow that limx→0e1/x−1e1/x+1 does not exist.
View Solutionlim_(xto0)(e^(1/x))/(e^((1/x)+1))=
View SolutionFind limit of the following if it exists:
limx→0e4x−1x
View SolutionFind limit of the following if it exists:
limx→0esin−1x
View Solution
