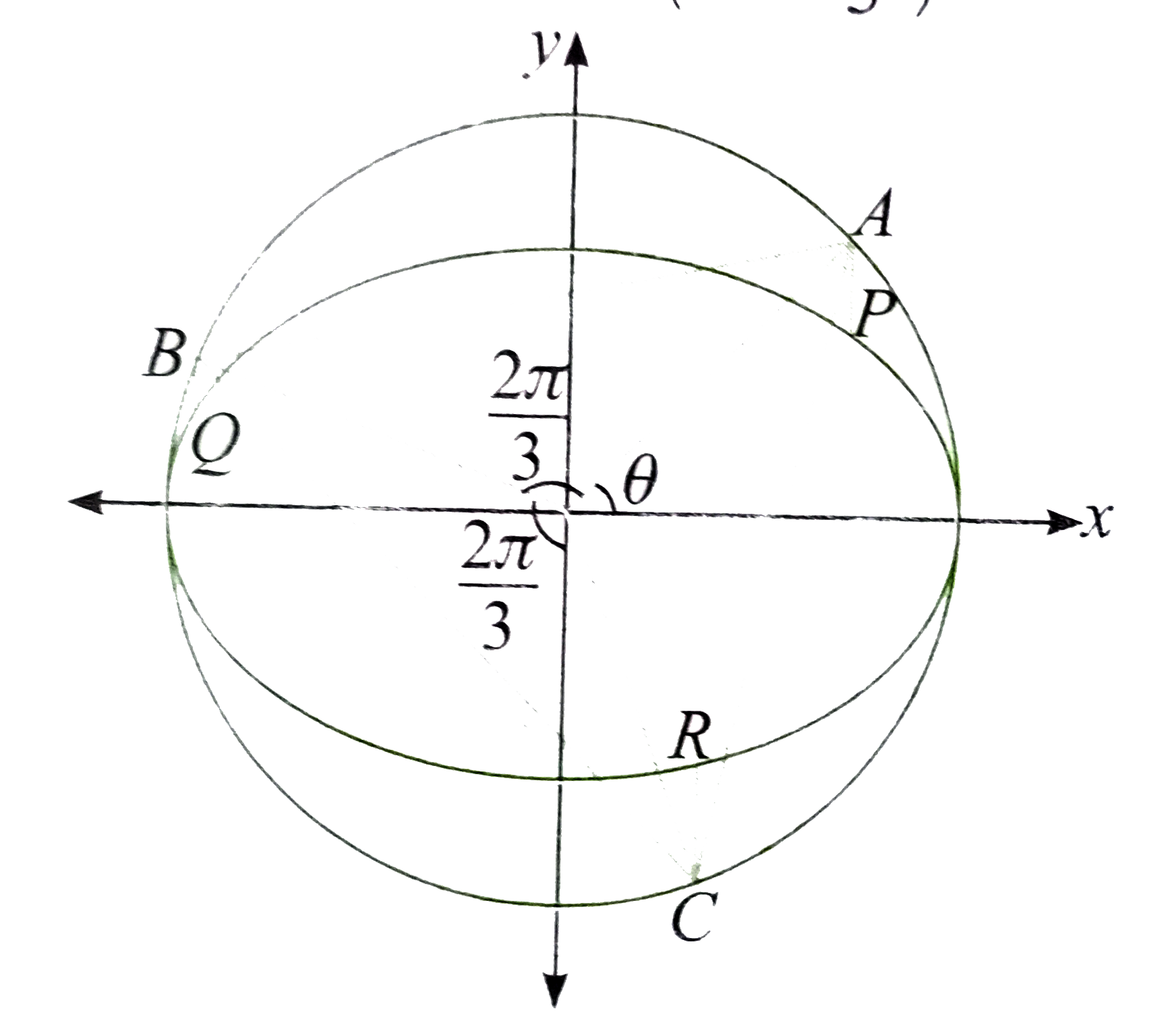
show that the area of the triangle inscribed in the circle $\frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1$ meet the ellipse respictively at P,Q,R so that P,Q,R lie on the same side of the major axis as A,B,C respictively. Prove that the normal to the ellipse drawn at the points P,Q and R are concurrent.

Video Solution

Text Solution

Verified by Experts

Let A , B and C, be the points on the cicle whose cooridnates are
$A (a cos θ, a sin θ)$
$B (a cos (θ + \frac{2 π}{3}), a sin (θ + \frac{2 π}{3}))$
$C (a cos (θ + \frac{4 π}{3}), a sin (θ + \frac{4 π}{3}))$
Hence, $P \equiv (a cos θ, b sin θ)$
$Q \equiv (a cos (θ + \frac{2 π}{3}), a sin (θ + \frac{2 π}{3}))$
$R \equiv (a cos (θ + \frac{4 π}{3}), a sin (θ + \frac{4 π}{3}))$
It is given that P,Q and R are on the same side of the x-axis as A,B, and C.
So, the required nomrmals ot the ellipse at P,Q and R are
$a x sec θ - by cosec θ = a^{2} - b^{2} (1)$
$a x sec (θ + \frac{2 π}{3} - by cosec (θ + \frac{2 π}{3}) = a^{2} - n^{2} (2)$
$a x sec (θ + \frac{4 π}{3} - by cosec (θ + \frac{4 π}{3}) = a^{2} - n^{2} (3)$

Now, $Δ$ = $∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sec θ & cosec θ & 1 sec (θ + \frac{2 π}{3}) & cosec (θ + \frac{2 π}{3}) & 1 sec (θ + \frac{2 π}{3}) & cosec (θ + \frac{2 π}{3}) & 1 \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
Multiplying $R_{1}, R_{2} and R_{3}$ , by $sin θ cos, θ, sin (θ + \frac{2 π}{3}) c o (θ + \frac{2 π}{3}) and sin (θ + \frac{4 π}{3})$ respectively, we get
$Δ = \frac{1}{k} ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ sin (θ + \frac{2 π}{3}) & cos (θ + \frac{2 π}{3}) & sin (2 θ + \frac{4 π}{3}) sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
Where
$k = 2 sin θ cos θ sin (θ + \frac{2 π}{3}) cos (θ - \frac{2 π}{3}) sin (θ + \frac{4 π}{3}) cos (θ + \frac{4 π}{3})$
Operating $R_{2} \to R_{2} + R_{3}$
$Δ = \frac{1}{k} ∣ ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ 2 sin θ \cdot cos . \frac{2 π}{3} & 2 cos θ \cdot cos . \frac{2 π}{3} & 2 sin θ \cdot cos . \frac{4 π}{3} sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣ ∣$
$= \frac{1}{k} ∣ ∣ ∣ ∣ ∣ \begin{matrix} sin θ & cos θ & sin 2 θ - sin θ & - cos θ & - sin θ sin (θ - \frac{2 π}{3}) & cos (θ - \frac{2 π}{3}) & sin (2 θ - \frac{4 π}{3}) \end{matrix} ∣ ∣ ∣ ∣ ∣$

|

Updated on:21/07/2023

Class 12 MATHS QUESTION BANK

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile