Show that the compound statements (p∨q)∧~p and ~p∧q are logically equivalent.
Video Solution
Text Solution
Truth values of (p∨q)∧~p and ~p∧q are as follows:
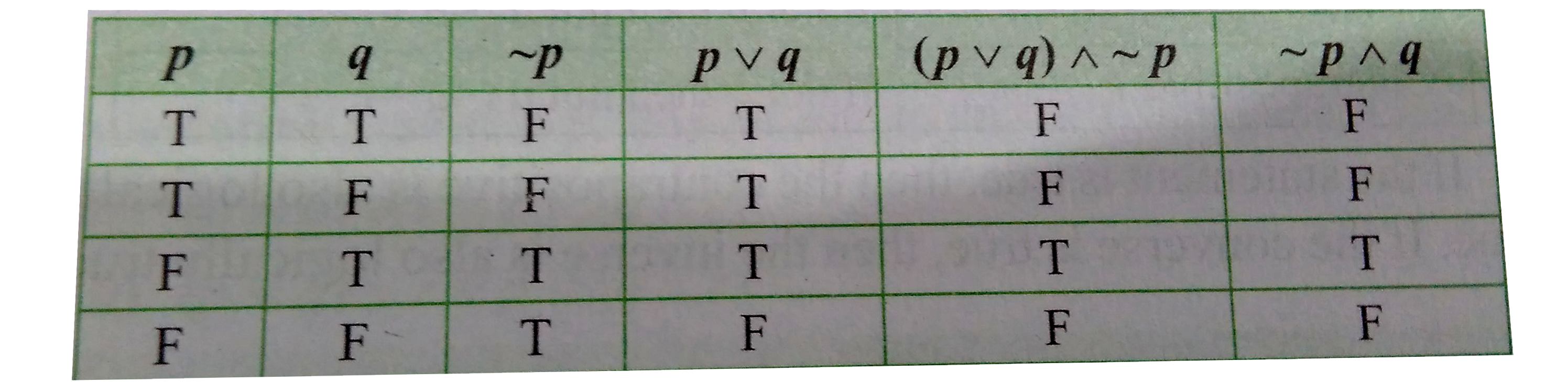
Clearly , (p∨q)∧~p and ~p∧q have identical truth values.
∴(p∨q)∧~p≡~p∧q
|
Topper's Solved these Questions
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:Exercise 10.1
Explore 8 Videos
- MATHMETICAL REASONINGBook:CENGAGEChapter:MATHMETICAL REASONINGExercise:Exercise 10.2
Explore 5 Videos
- LOGARITHM AND ITS PROPERTIESBook:CENGAGEChapter:LOGARITHM AND ITS PROPERTIESExercise:JEE Previous Year
Explore 5 Videos
- MATRICESBook:CENGAGEChapter:MATRICESExercise:Solved Examples And Exercises
Explore 165 Videos
Similar Questions
Knowledge Check
~p∧q is logically equivalent to
Ap→qBq→pC~(p→q)D~(q→p)~p∧q is logically equivalent to
Ap→qBq→pC~(p→q)D~(q→p)p→q is logically equivalent to
Ap∧~qB~p→~qC(p∨~q)Dnone of these
The compound statement (p→~q)∨(p∧q) is logically equivalent to
View SolutionThe compound statement (p→q)∨(p∧~q) is logically equivalent to
View Solutionp∧(q∧r) is logically equivalent to
View Solution~(p∨q)∨(~p∧q)is logically equivalent to
View Solutionp∧(p→q) is logically equivalent to
View Solution