Show that the diagonals of a parallelogram divide it into four triangles of equal area.
Video Solution
Text Solution
GIVEN A ||gm ABCD. Its diagonals AC and BD intersect at O.
TO PROVE ar(△OAB)=ar(△OBC)
=ar(△OCD)=ar(△OAD)
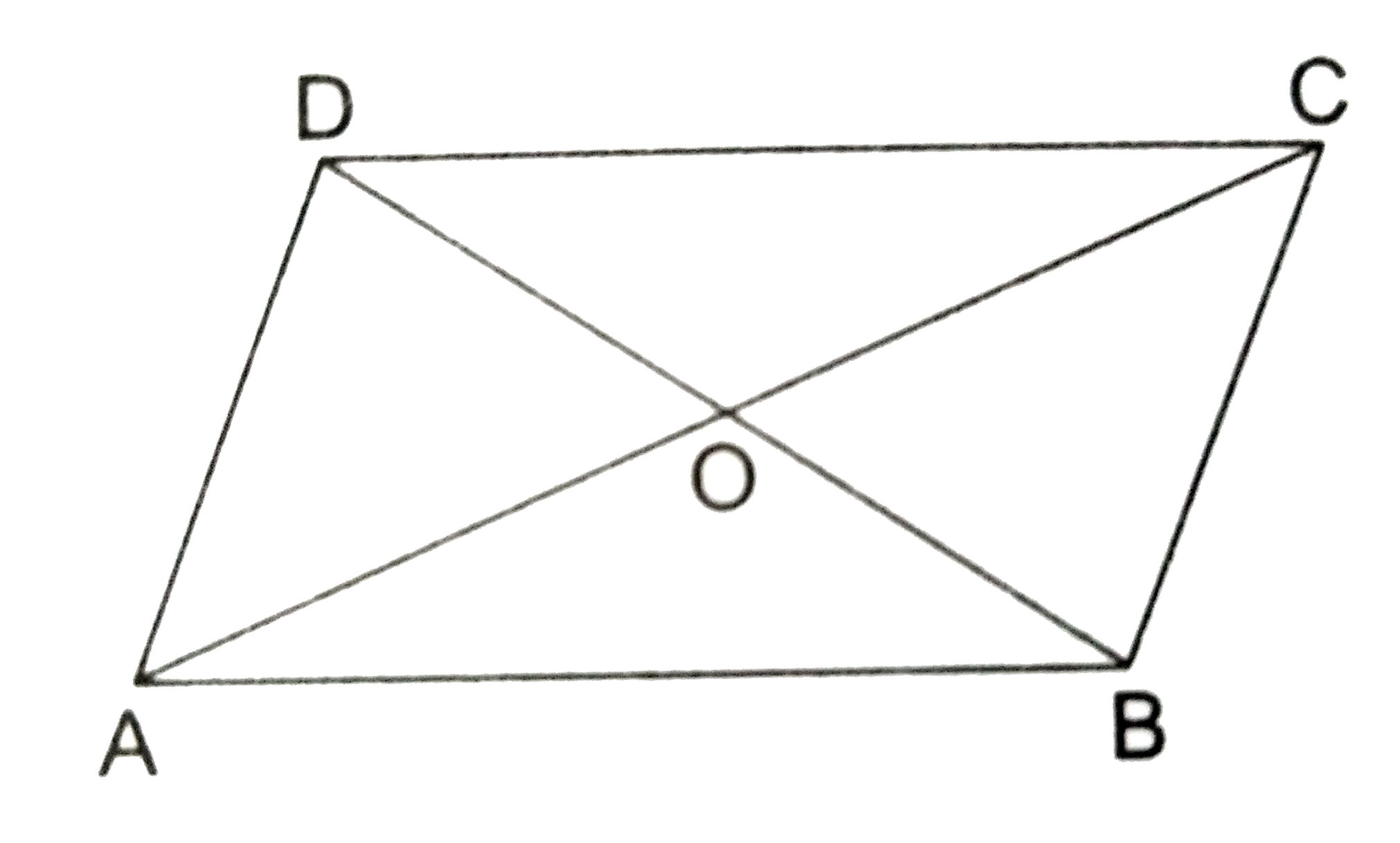
PROOF Since the diagonals of a ||gm bisect each other, we have
OA=OCandOB=OD.
Also, a median of a triangle divides it into two △ of equal area.
Now, in △ABC, BO is the median.
∴ar(△OAB)=ar(△OBC). ...(i)
In △ABD,AO is the median.
∴ar(△OAB)=ar(△OAD). ...(ii)
In △ACD,DO is the median.
∴ar(△OAD)=ar(△OCD). ...(iii)
From (i), (ii) and (iii), we get
∴ar(△OAB)=ar(△OBC). ...(i)
|
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Knowledge Check
Show that each diagonal of a parallelogram divide it into two congruent triangles.
The following are the steps involved in showing the above result. Arrange them in sequential order.
A) In △ABC and △CDA, AB=DC and BC=AD (∴ opposite angles of parallelogram) AC=AC (common side).
B) Let ABCD be a parallelogram. Join AC.
C) By SSS congruence property, △ABC≅△CDA.
D) Similarly, BD divides the triangle into two congruent triangles.ABACDBBDACCBADCDBDCAAsserion (A) : The diagonals of a ||gm divide it into four triangle of equal area.
Reason (R ) : A diagonal of a ||gm divides it into two triangle of equal area.ABoth Assertion (A) and Reason (R ) are true and Reason (R ) is a correct explansion of Assertion (A).BBoth Assertion (A) and Reason (R ) are true but Reason (R ) is not a correct explansion of Assertion (A).CAssertion (A) is true and Reason (R ) is false.DAssertion (A) is false and Reason (R ) is true.
A diagonal of a parallelogram divides it into two congruent triangles.
View SolutionA diagonal of parallelogram divides it into two congruent triangles.
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area. GIVEN : A parallelogram ABCD in which BD is one of the diagonals. TO PROVE : ar (ABD)=ar(CDB)
View SolutionThe diagonals of a parallelograms are equal .
View SolutionShow that a median of a triangle divides it into two triangles of equal areas.
View SolutionShow that a median of a triangle divides it into two triangles of equal area.
View Solution
