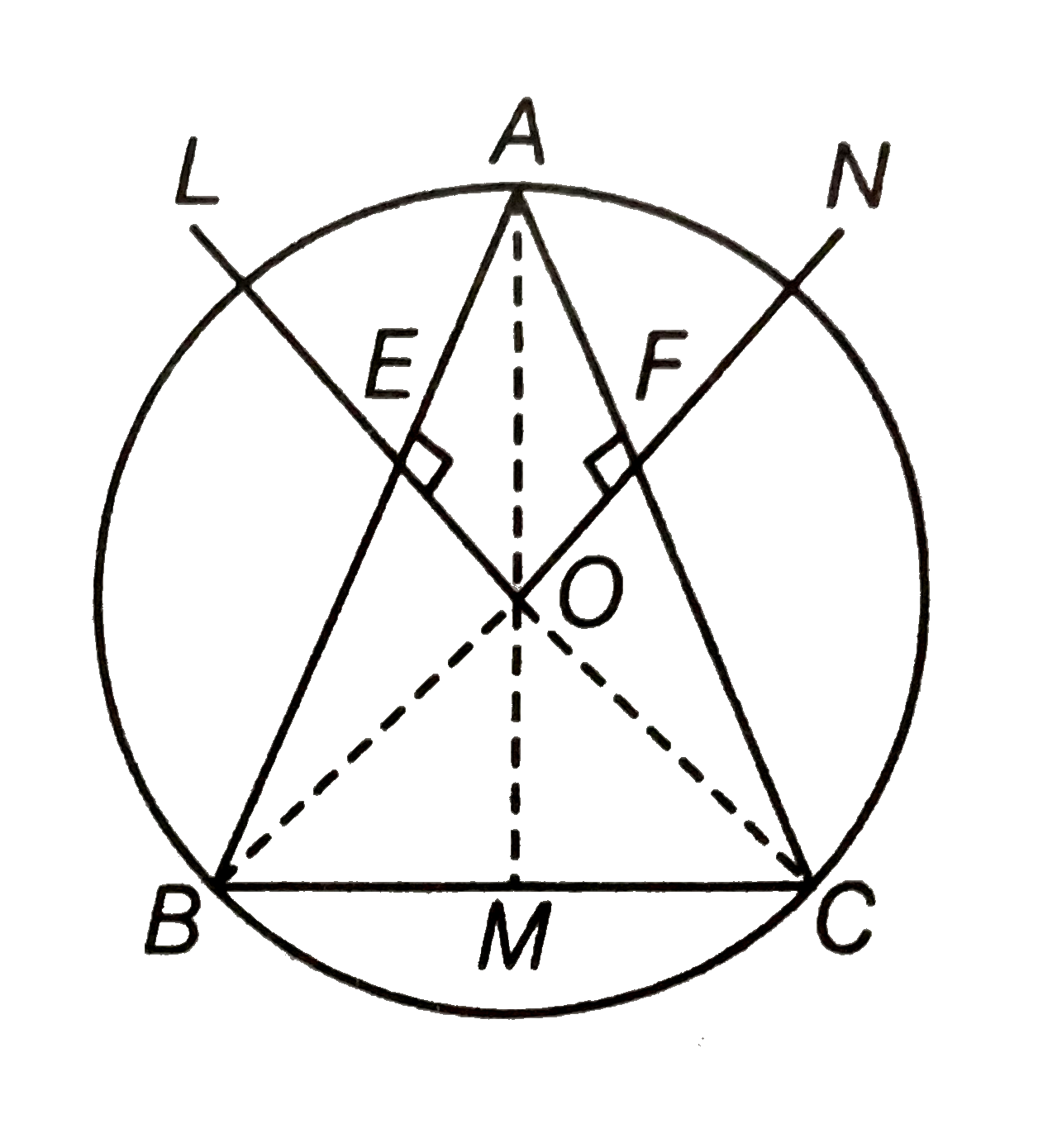
Show that the perpendicular bisectors of the sides of a triangle are concurrent.

Video Solution

Text Solution

Verified by Experts

Let D,E,F be the midpoints of the sides BC,CA and AB of $△ A B C$ .
Let the perpendicular bisectors of the sides BC and AC meet each other in the points O. Choose O as the origin and let $¯ a, ¯ b, ¯ c, ¯ d, ¯ e, ¯ f$ be the position vectors of the points A,B,C,D,E,F respectively.
Here we have to prove that $¯ ¯¯¯¯ ¯ O F = ¯ f$ is perpendicular to $¯ ¯¯¯¯ ¯ A B = ¯ b - ¯ a$ .
By the midpoint formula, $¯ d = \frac{¯ b + ¯ c}{2}, ¯ e \frac{¯ c + ¯ a}{2}, ¯ f = \frac{¯ a + ¯ b}{2}$
Now, $¯ ¯¯¯¯ ¯ O D = ¯ d$ is perpendicular to $¯ ¯¯¯¯ ¯ B C = ¯ c - ¯ b$ .
$∴ ¯ d \cdot (¯ c - ¯ b) = 0 ∴ (\frac{¯ b + ¯ c}{2}) \cdot (¯ c - ¯ b) = 0$
$∴ (¯ c + ¯ b) \cdot (¯ c - ¯ b) = 0$
$∴ ¯ c \cdot ¯ c + ¯ b \cdot ¯ c - ¯ c \cdot ¯ b - ¯ b \cdot ¯ b = 0$
$∴ c^{2} - b^{2} = 0 ∴ c^{2} = b^{2} . . . [∵ ¯ c \cdot ¯ c = c^{2}, ¯ b \cdot ¯ b = b^{2} and ¯ c \cdot ¯ b = ¯ b \cdot ¯ c]$ . . .(1)
Also, $¯ ¯¯¯¯ ¯ O E = ¯ e$ is perpendicular to $¯ ¯¯¯¯ ¯ A C = ¯ c - ¯ a$
$∴ ¯ e \cdot (¯ c - ¯ a) = 0$
$∴ (\frac{¯ c + ¯ a}{2}) \cdot (¯ c - ¯ a) = 0 ∴ as above c^{2} = a^{2}$ . . . .(2)
From (1) and (2), we get,
$b^{2} = a^{2} ∴ b^{2} - a^{2} = 0$
$∴ (¯ b + ¯ a) \cdot (¯ b - ¯ a) = 0$
$∴ (\frac{¯ b + ¯ a}{2}) \cdot (¯ b - ¯ a) = 0$
$∴ ¯ f = ¯ ¯¯¯¯ ¯ O F$ is perpendicular to $¯ b - ¯ a = ¯ ¯¯¯¯ ¯ A B$ .
$∴$ the perpendicular bisectors of the sides of $Δ A B C$ are concurrent.

Updated on:21/07/2023