Show that the segment joining the mid-points of a pair of opposite sides of a parallelogram, divides it into two equal parallelograms.
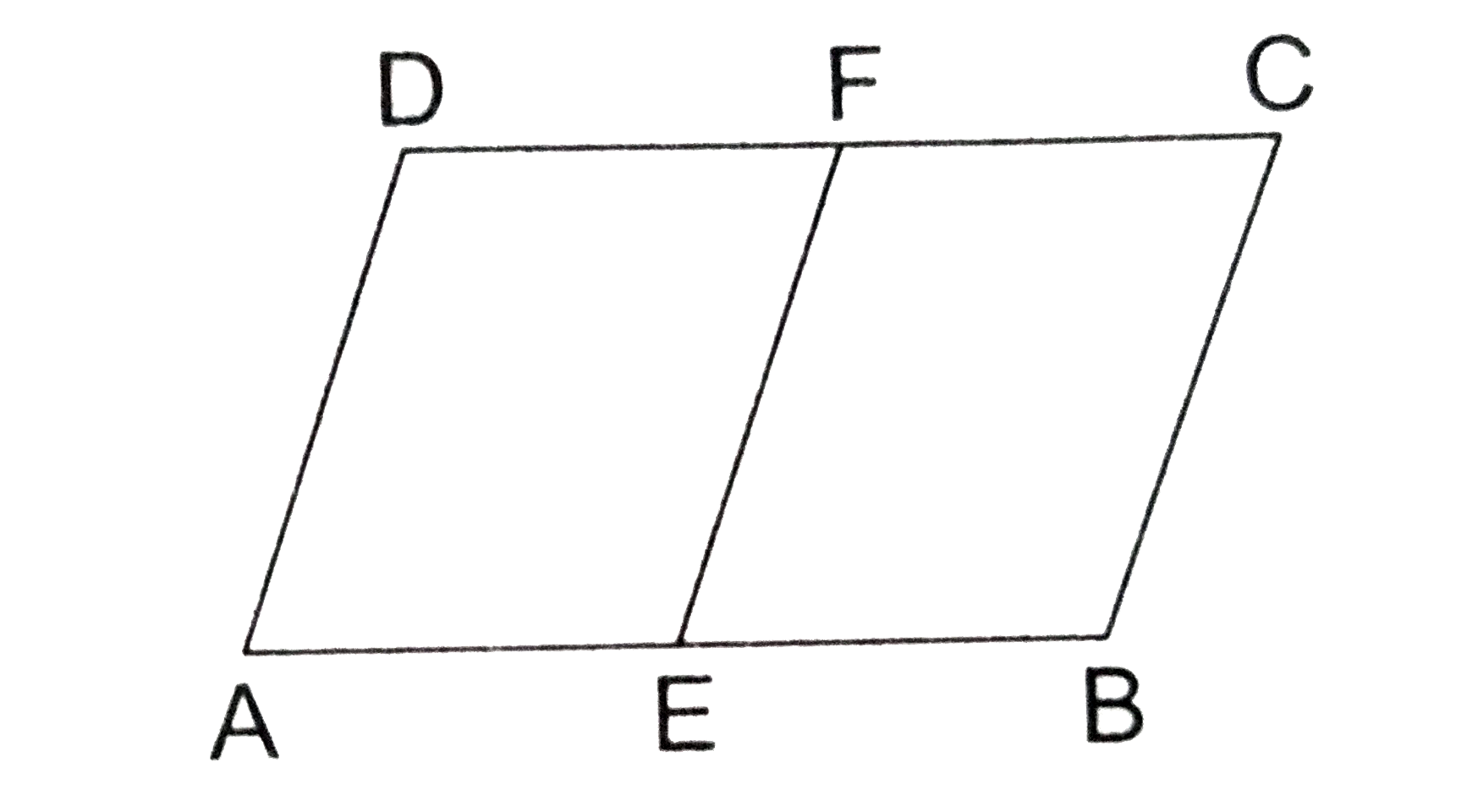
GIVEN A ||gm ABCD in which E and F are the midpoints of AB and DC respectively. E and F are joined.
TO PROVE
PROOF Since ABCD is a ||gm, we have AB||DC
and AB = DC.
AEFD is a ||gm.
Again, EB||FC and EB = FC
EBCF is a ||gm.
Now, AEFD and EBCF being two parallelograms with equal bases and between the same parallels, they must have equal areas.
Topper's Solved these Questions
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - Exercise 11
38 Videos
- AREAS OF PARALLELOGRAMS AND TRIANGLES BOOK - RS AGGARWALCHAPTER - AREAS OF PARALLELOGRAMS AND TRIANGLES EXERCISE - MULTIPLE-CHOICE QUESTIONS (MCQ)
32 Videos
- AREAS OF TRIANGLES AND QUADRILATERALSBOOK - RS AGGARWALCHAPTER - AREAS OF TRIANGLES AND QUADRILATERALSEXERCISE - Multiple Choice Questions (Mcq)
16 Videos
Similar Questions
Show that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionA diagonal of a parallelogram divides it into two triangles of equal area.
View SolutionShow that the lines joining the mid-points of opposite sides of a quadrilateral bisect each other.
View SolutionThe opposite angles of a parallelogram are equal.
View SolutionThe opposite angle of a parallelogram are equal.
View SolutionUsing vector method, prove that the line segments joining the mid-points of the adjacent sides of a quadrilateral taken in order form a parallelogram.
View SolutionProve that the figure formed by joining the mid-points of the pairs of consecutive sides of a quadrilateral is a parallelogram.
View SolutionIf the adjacent sides of a parallelogram are equal then parallelogram is a
View Solution
