Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is cos−11√3
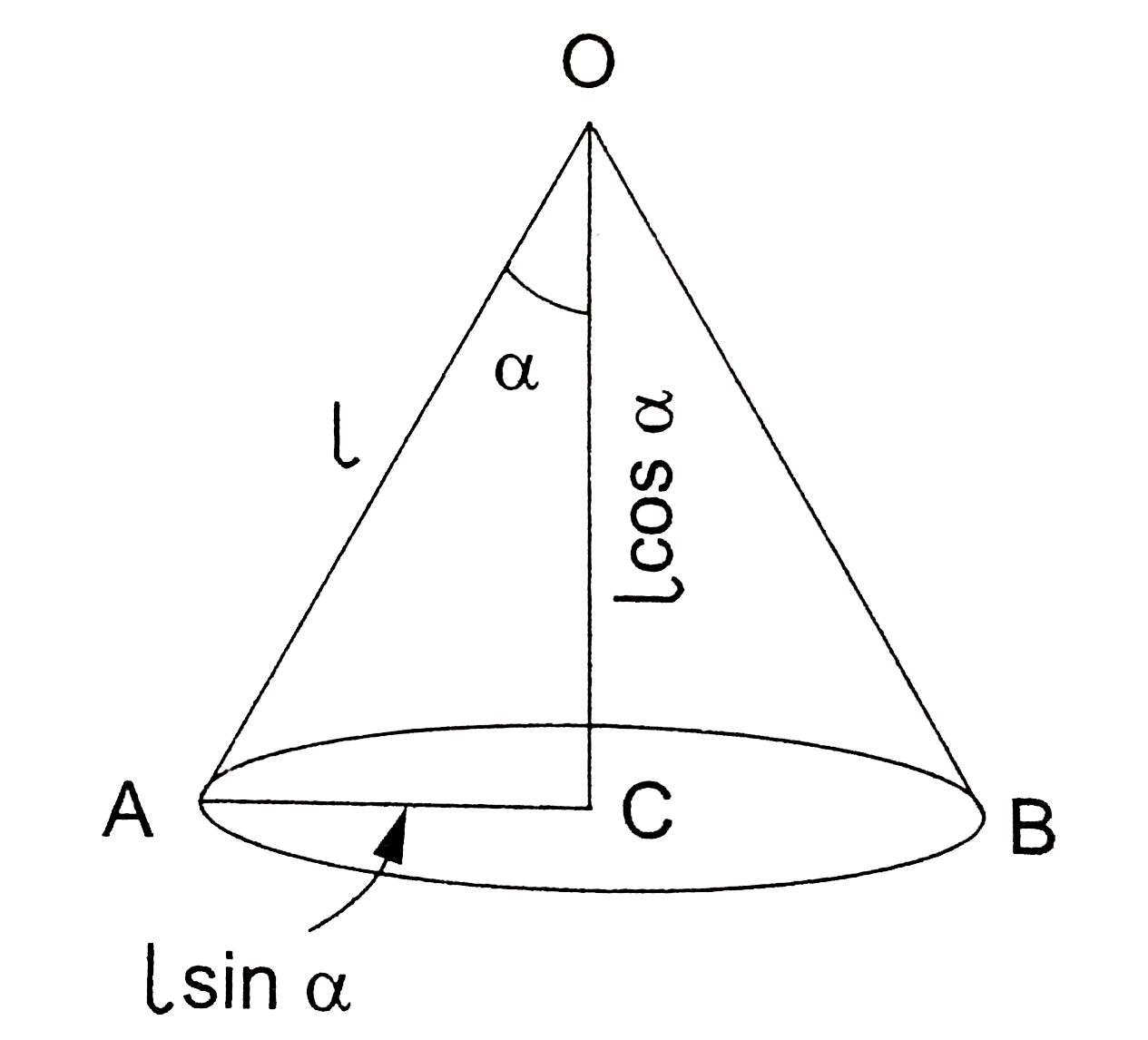
Let α be the semivertical angle of a cone of given slant height l. Then, height of the cone =lcosα, radius of the base =lsinα. Let V be the volume of the cone. Then,
V=13πr2h=13π(l2sin2α)(lcosα)
or V=13πl3sin2αcosα
∴dVdα=13πl3(−sin3α+2sinαcos2α)=13πl3sinα(2cos2α−sin2α)
And, d2Vdα2=13πl3cosα(2cos2α−sin2α)+13πl3sinα(−4sinαcosα−2sinαcosα)
=13πl3cos3α(2−7tan2α)
Now, for a maxima or minima, we have dVdα=0
Now, dVdα=0⇒13πl3sinα(2cos2α−sin2α)=0
⇒sinα=0or2cos2α−sin2α=0
⇒α=0orα=tan−1√2
Neglecting α=0, we have α=tan−1√2, i.e., tanα=√2
Now, tanα=√2⇒sec2α=3⇒cosα=1√3⇒α=cos−1.1√3
∴[d2Vdα2]α=tan−1√2=13πl3.(1√3)3(2−14)=−4πl33√3<0
Thus, V is maximum when α=cos−1.1√3, i.e., when the semivertical angle of the cone is cos−11√3
Topper's Solved these Questions
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11A
Explore 21 Videos
- APPLICATIONS OF DERIVATIVESBook:RS AGGARWALChapter:APPLICATIONS OF DERIVATIVESExercise:Exercise 11B
Explore 17 Videos
- ADJOINT AND INVERSE OF A MATRIXBook:RS AGGARWALChapter:ADJOINT AND INVERSE OF A MATRIXExercise:Exercise 7
Explore 37 Videos
- AREA OF BOUNDED REGIONS Book:RS AGGARWALChapter:AREA OF BOUNDED REGIONS Exercise:Exercise 17
Explore 39 Videos
Similar Questions
Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan−1√2.
View SolutionShow that the semi - vertical angle of the right - circular cone of maximum volume and of given slant height is :
(i) tan−1√2
(ii) cos−11√3.
View SolutionProve that the semi-vertical angle of the right circular cone of given volume and least curved surface is cot−1(√2).
View SolutionShow that the height of the cylinder of maximum volume that can be inscribed in a cone of height h is 13h
View SolutionShow that semi-vertical angle of right circular cone of given surface area and maximum volume is sin−1(13).
View Solutionshow that the semi vertical angle of a right circular cone of given total surface area and max volume is sin−1(13)
View SolutionThe semi-vertical angle of the cone of maximum curved surface area that can be inscribed in a given sphere of radius R is: (A) tan−1(12) (B)tan−1(1√2) (C) tan−1(12√2) (D) tan−1(14)
View SolutionIf h be the height and α the semi vertical angle of a right -circular cone, the its volume is given by
View SolutionShow that height of the cylinder of greatest volume which can be inscribed in a right circular cone of height h and semi vertical angle is one-third that of the cone and the greatest volume of cylinder is 427πh3tan2α.
View SolutionThe volume of a right circular cone of height 3 cm and slant height 5 cm is
View Solution
