show that the tangents to the curve y=2x3−3 at the point where x=2 and x=-2 are parallelSolution in Bengali
The correct Answer is:A, B, C, D
a. Area =2(121×1)=1 sq. units.

b. y2=x3and|y|=2x, both the curve are symmetric about y-axis

4x2=x3orx=0,4.
Required area =24∫0(2x−x3/2)dx=325 sq. units.
c. √x+√|y|=1
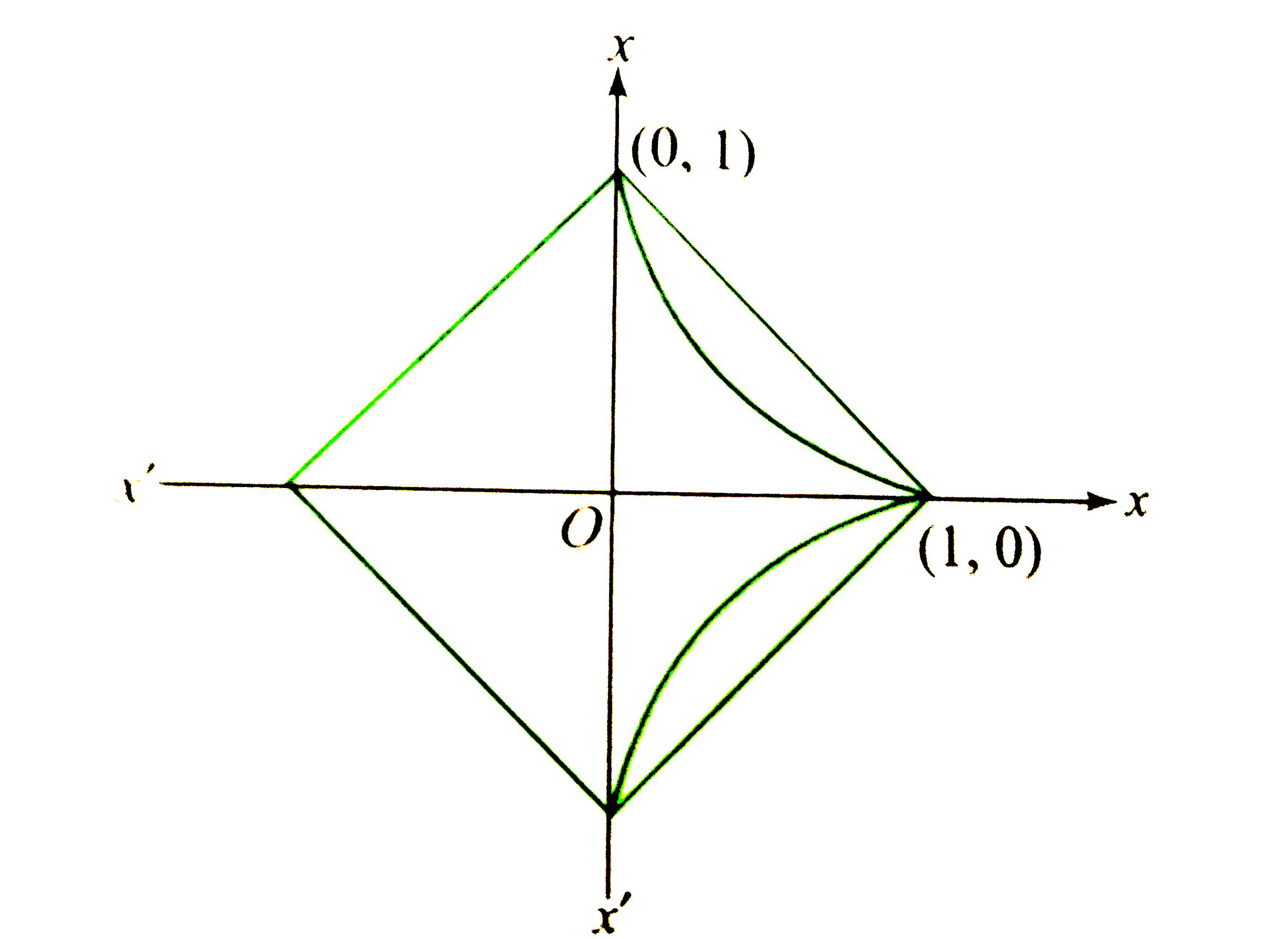
The curve is symmetrical about x-axis
√|y|=1−√xand√x=1−√|y|
⇒ for x>0,y>0√y=1−√x
12√ydydx=−12√x
dydx=−√yx
dydx<0, function is decreasing
Required area =21∫0((1−x)−(1−2√x+x))dx
=41∫0(√x−x)dx
=4[x3/23/2−x22]10
=4[23−12]
=23 sq. units.
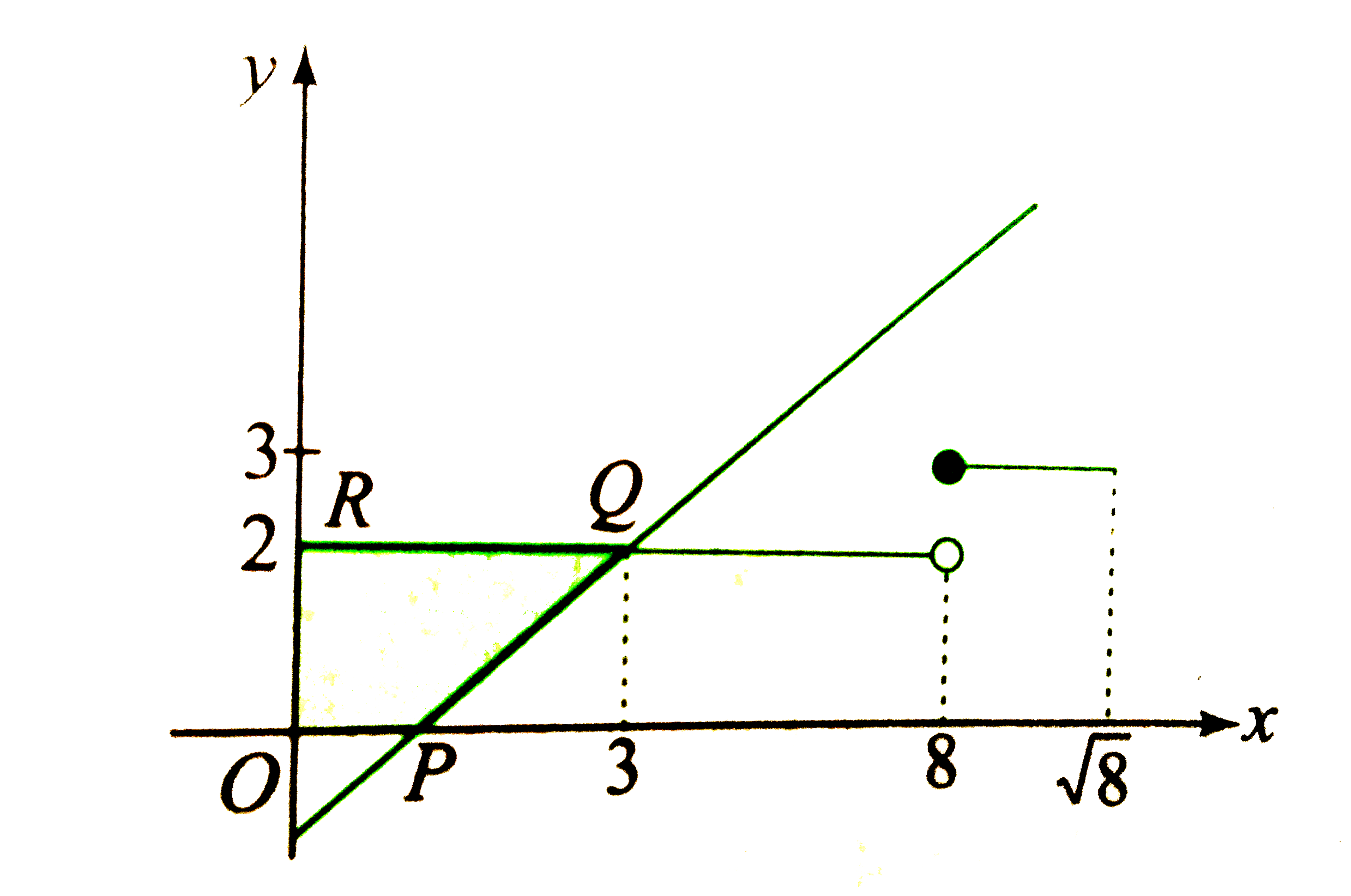
d. If −8<x<8, then y=2.
If x∈(−8√2,−8]∪[8,8√2), then y=3, and so on
Intersection of y=x−1andy=2. We get x=3∈(−8,8).
Intersection of y=x−1andy=3.
We get x=4∉(−8√2,−8]∪[8,8√2).
Similarly, y=x−1 will not intersect y=[x264+2] at any
other integral, except in the interval x∈(−8,8).
Required area (shaded region ) =2×3−12×2×2
=4 sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Numerical Value Type
18 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Archives
10 Videos
- AREABOOK - CENGAGE PUBLICATIONCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE PUBLICATIONCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Subjective Type
2 Videos
- BINOMIAL THEOREMBOOK - CENGAGE PUBLICATIONCHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
Similar Questions
The area enclosed by the curve c:y=x√9−x2(x≥0) and the x-axis is________
View SolutionThe area of the figure bounded by the parabola (y−2)2=x−1, the tangent to it at the point with the ordinate x=3, and the x−aξs is 7sq.unites (b) 6sq.unites 9sq.unites (d) None of these
View SolutionLet Ar be the area of the region bounded between the curves y2=(e−kr)x(where k>0,r∈N) and the line y=mx(where m≠0), k and m are some constants
A1,A2,A3,… are in G.P. with common ratio
View SolutionProve that for λ>1, the equation xlogx+x=λ has least one solution in [1,λ].
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionFind the point on the curve y=x3−x2−x+3, where the tangent is parallel to x-axis .
View SolutionFind the points on the curve x3−2x2−2x at which the tangent lines are parallel to the line y=2x−3 .
View SolutionFind the point on the curve y=x2−2x+3 , where the tangent is parallel to x-axis.
View SolutionFind the points on the curve y=x3−2x2−x, where the tangents are parallel to 3x−y+1=0
View SolutionShow that the tangents to the curve y=2x3−4 at the points x=2andx=−2 are parallel
View SolutionShow that the tangent to the curve 8y=(x−2)2 at the point (-6, 8) is parallel to the tangent to the curve y=x+(3/x) at the point (1, 4).
View Solutionवक्र y=x3−x2−x+3 के उन बिन्दुओ को ज्ञात करें जहां स्पर्श रेखा x− अक्ष के समान्तर है |
View Solutionसिद्ध कीजिए की वक्र y=2x3−3 के उन बिन्दुओ पर स्पर्श रेखाएँ समांतर है, जहाँ x=2 और x=−2 है .
View Solutionवक्र y=x3−2x2+x−2 पर , उन बिन्दुओ को मालूम करे जिन पर की स्पर्शरेखा X - अक्ष के समांतर हो |
View SolutionThe points on the curve y=x3−2x2−x, where the tangents are parallel to 3x-y+1=0 are
View Solutionवक्र x2+y2−2x−3=0 के उन बिन्दुओ पर स्पर्श रेखाओ के समीकरण ज्ञात कीजिए जहाँ पर वे X - अक्ष के समान्तर है।
View Solution
