σ2X,σ2Yandσ2X−Y are the variances of X, Y and X−Y respectively, then rXY is
A
σ2X+σ2Y−σ2X−Y2σ2σY
B
σ2X+σ2YσXσY
C
σ2X−σ2Yσ2X+σ2Y
D
σXσYσX−Y
Text Solution
The correct Answer is:A
|
Topper's Solved these Questions
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:PROBLEM SET (1) TRUE/FALSE
Explore 6 Videos
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:PROBLEM SET (1) (FILL IN THE BLANKS)
Explore 10 Videos
- CORRELATION AND REGRESSION Book:ML KHANNAChapter:CORRELATION AND REGRESSION Exercise:QUESTION (STATE GIVING REASONS, WHETHER EACH OF THE FOLLOWING STATEMENTS IS TRUE OR FALSE)
Explore 10 Videos
- CONCEPTS OF SET THEORY Book:ML KHANNAChapter:CONCEPTS OF SET THEORY Exercise:Self Assessment Test
Explore 13 Videos
- DEFINITE INTEGRALBook:ML KHANNAChapter:DEFINITE INTEGRALExercise:Miscellaneous Questions (Assertion/Reason)
Explore 1 Video
Similar Questions
Given r=0.8,Σxy=60,σy=2.5 and Σx2=90, find the number of items, if x and y are deviation from their respective means.
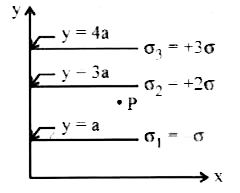
View SolutionThree infinite long plane sheets carrying uniform charge densities σ1=−σ,σ2=+2σandσ3=3σ are placed parallel to the x-z plane at y=a,y=3aandy=4a as shown in the figure. What is the electric field at point 'P' ?
View Solution
Knowledge Check
If means ¯¯¯X,¯¯¯Y of the variates X and Y are eah zero and σ2X=σ2Y=1andr=rXY≠1, the value of b such that X+YandX+bY are uncorrelated is
Ab=0Bb=1Cb=−1Dnone of theseIf σx=3,σy=4, and bxy=13, then the value of r is
A14B94C49D4x1andx2 are two variates with variances σ21andσ22 respectively and r is the correlation between them. The value of a such that x1+ax2 and x1+σ1σ2x2 are uncorrelated is
A−σ1σ2Brσ2σ1Cσ1σ2Dnone of these
If Σ2nr=1sin−1xr=nπ,thenΣ_(r=1)2nxr is equal to
View SolutionIf Σnr=1cos−1xr=0,thenΣnr=1xr equals
View SolutionGiven r=0.8,Σxy=60,σy=2.5andΣx2=90. Find the number of items (x and y are deviations from arithmetic average)
View SolutionIf Σ2nr=1sin−1xr=nπ,thenΣ_(r=1)2nxr is equal to
View SolutionIf Σnr=1cos−1xr=0,thenΣnr=1xr equals
View Solution
