Question

Similar Triangles and their properties

Explanation

Similar Triangles and their Properties

In this chapter, we will focus on similar triangles and their properties.  We will also have a look at the similar triangles theorem along with solved examples that would help in getting the perfect knowledge about it. Well, when we say similar triangles, it refers to the triangles that possess the same shape, but there is the variation of size. Examples of similar objects are squares of any side lengths or all equilateral triangles. It can be understood that when two triangles are similar, then the corresponding sides are in equal proportion and their corresponding angles are also congruent. The symbol, ‘~’ is used in denoting the similarity of triangles. Here we can consider a hula hoop and wheel of a cycle. It should be noted that there are similarities in both the shapes of the objects.

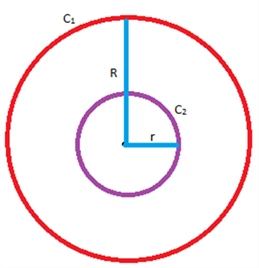
Consider the above circle C₁ and C₂ where the radiuses are R and r, respectively. Although the shapes are the same, it does not have the same size. So, in this case, it can be said that C₁ ~ C₂. So, two circles are always similar irrespective of their diameter. So, if we look at the condition for the similarity of triangles, then they are as follows:

i) Corresponding angles of both the triangles are equal, and

ii) Corresponding sides of both the triangles are in proportion to each other as well.

Similar Triangle Example

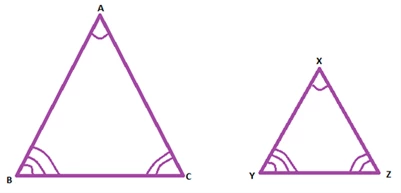
Consider the above figure where you can see that the two triangles ΔABC and ΔXYZ are similar only if,

1. ∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z


2. AB/XY = BC/YZ = AC/XZ

In case the conditions mentioned above are satisfied, then it would be right to say that ΔABC ~ ΔXYZ

It is quite interesting to note that if there is an equal corresponding angle of two triangles, then those triangles are known as equiangular triangles.

Properties of Similar Triangles

• Both have the same shape but not the same sizes


• It is equal when it comes to each pair of corresponding angles


• The ratio is the same as the corresponding sides

Similar triangle formula

It is possible to find out the dimensions of one triangle if two triangles are similar. Suppose ABC and XYZ are two similar triangles, then we can find the relevant angles and side length with the help of the below-given expressions or formulas.

• ∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z


• AB/XY = BC/YZ = AC/XZ

Similar triangles Theorems with Proofs

It is important to learn the theorems that are used in solving similar triangles problems. So, we will now study this along with proof.

AA (or AAA) or Angle-Angle Similarity

Angle-Angle Similarity - The two triangles are found to be similar to each other if any two angles of a triangle are equal to any two angles of another triangle.

When we look at the figure above, if ∠ A = ∠X and ∠C = ∠Z then ΔABC ~ ΔXYZ.

Thus it can be said that:

AB/XY = BC/YZ = AC/XZ

and ∠B = ∠Y

SAS or Side-Angle-Side Similarity

Side-Angle-Side Similarity - When there is an equal proportion of the two sides of a triangle with two angles of another triangle, then the triangles are said to be similar.

So, here,

if ∠A = ∠X and AB/XY = AC/DF then ΔABC ~ΔXYZ.

So, from the congruency, it can be stated that,

AB/XY = BC/YZ = AC/XZ

and ∠B = ∠Y and ∠C = ∠Z

SSS or Side-Side-Side Similarity

Side-Side-Side Similarity - The two triangles are similar if the entire three sides are in proportion to the three sides of another triangle.

Here, if AB/XY = BC/YZ = AC/XZ then ΔABC ~ΔXYZ.

From this result, it can be stated that

∠A = ∠X, ∠B = ∠Y and ∠C = ∠Z

Related Videos:

• Criteria for Similarity of Triangles, Properties of Similar Triangle


• More on Characteristics Properties, Areas of Two Similar Triangles


• How similarity is different from congruence


• Similar Polygons


• Basic proportionality Theorem or Thales Theorem


• Converse of Basis proportionality theorem

Now, let us have a look at some of the examples of similar triangles to get more insights to it

Problem 1: It’s given that △ DEF ~△ MNK. If DE= 7 and MN=8. Can you find A(△DEF)/A(△MNK)?

Answer: A(△DEF)/A(△MNK)=DE²/MN²  (areas of similar triangles)

Therefore 7²/8² =49/64

Problem 2:   Q.1: In the ΔABC length of the sides are given as AP = 5 cm , PB = 10cm and BC = 20 cm.Also PQ||BC. Can you find PQ?

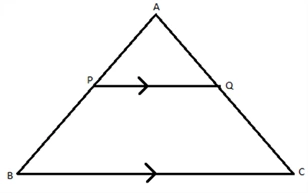
Solution: We can find that ΔABC and ΔAPQ, ∠PAQ is common where ∠APQ = ∠ABC (corresponding angles)

⇒ ΔABC ~ ΔAPQ (AA criterion for similar triangles)

⇒ AP/AB = PQ/BC

⇒ 5/15 = PQ/20

⇒ PQ = 20/3 cm

Problem 3: If ΔABC ~ ΔRST, use the indicated measures of ∠B and ∠C are 80⁰ and 47⁰ to find the measures of the remaining sides and angles of each of the triangles.

Solution: You need to measure of the third angle in ΔABC, including all three angles of ΔRST, as well as the lengths AC and ST. The sum of the interior angles of a triangle is 180º. Therefore, you can find m∠A very easily as under:

m∠A + m∠B + m∠C = 180º

m∠A + 80º + 47º = 180º

m∠A = 53º

As you can find that the corresponding angles are congruent, you know that m∠R = 53º, m∠S = 80º and m∠R = 47º. Using your proportionalities, you have

^AB/_RS = ^BC/_ST = ^AC/_RT

You can look forward to substituting the known values into the proportionality so as to find the value of ST:

³/₆ = ⁴/_ST

3(ST) = 24

ST = 8

To determine AC, you need to use the other half of the proportionality:

³/₆ = ^AC/₁₀

6(AC) = 30

AC = 5

Problem 4: The vertices of triangles ABC and PQR are defined by the coordinates: A(-2,0), B(0,4), C(2,0), P(-1,1), Q(0,3), and R(1,1).  Can you show that the two triangles are similar?

Solution: As we know the coordinates of the vertices, it would be possible to calculate the length of the sides of the two angles. For this, we need to follow these steps as under:

AB = √ ( 4 ² + 2 ² ) = 2 √5

BC = √ ( (-4) ² + 2 ² ) = 2 √5

CA = √ ( 4 ² ) = 4

PQ = √ ( 2 ² + 1 ² ) = √5

QR = √ ( (-2) ² + 1 ² ) = √5

RP = √ ( 2 ² ) = 2

By calculating the ratios of the lengths of the corresponding sides, we get

AB / PQ = 2, BC / QR = 2 and CA / RP = 2.

So, it can be written as AB / PQ = BC / QR = CA / RP = 2.

Important Chapters:

• NCERT Solutions for Maths


• NCERT Solution for Class 9 Maths Chapter Triangles


• NCERT Solution for Class 10 Maths Chapter Triangles