sinπ900{10∑r=1(r−ω)(r−ω2)} =
−1
0
1
√3/2
The correct Answer is:C
To solve the given problem, we need to evaluate the expression:
sin(π90010∑r=1(r−ω)(r−ω2))
where ω is a complex cube root of unity. Let's break this down step by step.
Step 1: Expand the product (r−ω)(r−ω2)
Using the distributive property, we can expand the product:
(r−ω)(r−ω2)=r2−rω−rω2+ωω2
Since ω and ω2 are roots of unity, we know that:
ω⋅ω2=ω3=1
Thus, we can simplify the expression:
(r−ω)(r−ω2)=r2−r(ω+ω2)+1
Step 2: Use the property of cube roots of unity
From the properties of cube roots of unity, we know:
1+ω+ω2=0⟹ω+ω2=−1
Substituting this back into our expression gives:
(r−ω)(r−ω2)=r2+r+1
Step 3: Sum the expression from r=1 to 10
Now we need to compute the sum:
10∑r=1(r2+r+1)
This can be broken down into three separate sums:
10∑r=1r2+10∑r=1r+10∑r=11
Step 4: Calculate each sum
1. Sum of squares: The formula for the sum of squares of the first n natural numbers is:
n∑r=1r2=n(n+1)(2n+1)6
For n=10:
10∑r=1r2=10⋅11⋅216=385
2. Sum of first n natural numbers: The formula for the sum of the first n natural numbers is:
n∑r=1r=n(n+1)2
For n=10:
10∑r=1r=10⋅112=55
3. Sum of 1: Since we are summing 1 for 10 terms:
10∑r=11=10
Step 5: Combine the results
Now, we can combine these results:
10∑r=1(r2+r+1)=385+55+10=450
Step 6: Substitute back into the sine function
Now we substitute back into the sine function:
sin(π900⋅450)=sin(450π900)=sin(π2)
Step 7: Evaluate the sine function
We know that:
sin(π2)=1
Final Answer
Thus, the final answer is:
sin(π90010∑r=1(r−ω)(r−ω2))=1
Topper's Solved these Questions
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (2) (True and False )
4 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (2) (Fill in the blanks)
2 Videos
- COMPLEX NUMBERS BOOK - ML KHANNACHAPTER - COMPLEX NUMBERS EXERCISE - Problem Set (1) (True and False)
5 Videos
- CO-ORDINATE GEOMETRY OF THREE DIMENSIONBOOK - ML KHANNACHAPTER - CO-ORDINATE GEOMETRY OF THREE DIMENSIONEXERCISE - SELF ASSIGNMENT TEST
11 Videos
- CONCEPTS OF SET THEORY BOOK - ML KHANNACHAPTER - CONCEPTS OF SET THEORY EXERCISE - Self Assessment Test
13 Videos
Similar Questions
Knowledge Check
n−1∑r=1sin2rπn equals
An2Bn−22Cn−12DnoneIn the circuit shown, E1=7V,E2=7V,R1=R2=1Ω and R3=3Ω respectively. The current through the resistance R3
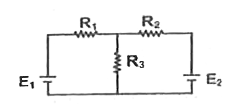 A0.083333333333333B3.5 AC1.75 ADnone of these
A0.083333333333333B3.5 AC1.75 ADnone of theseIn the R1=10Ω,R2=20Ω,R3=40ΩR4=80Ω and VA=5V,VB=10V,Vc=20V,VD=15V The current in the resistance R1 will be
 A0.4A toward OB0.4A away from OC0.8A toward OD0.8A toward O
A0.4A toward OB0.4A away from OC0.8A toward OD0.8A toward O
limn→∞n∑r=2((r+1)sinπr+1−rsinπr)
View SolutionIf in the figure R1=10Ω,R2=40Ω,R3=30Ω,R4=20Ω,R5=60Ω and a 12 V battery is connected to the arrangement, calculate (i) the total resistance in the circuit and (ii) the total current flowing in the circuit.
View SolutionIf x=Rsinωt+Rωt and y=Rcos(ωt)+R (where ω and R are constants), what are x and y components of acceleration when y is minimum ?
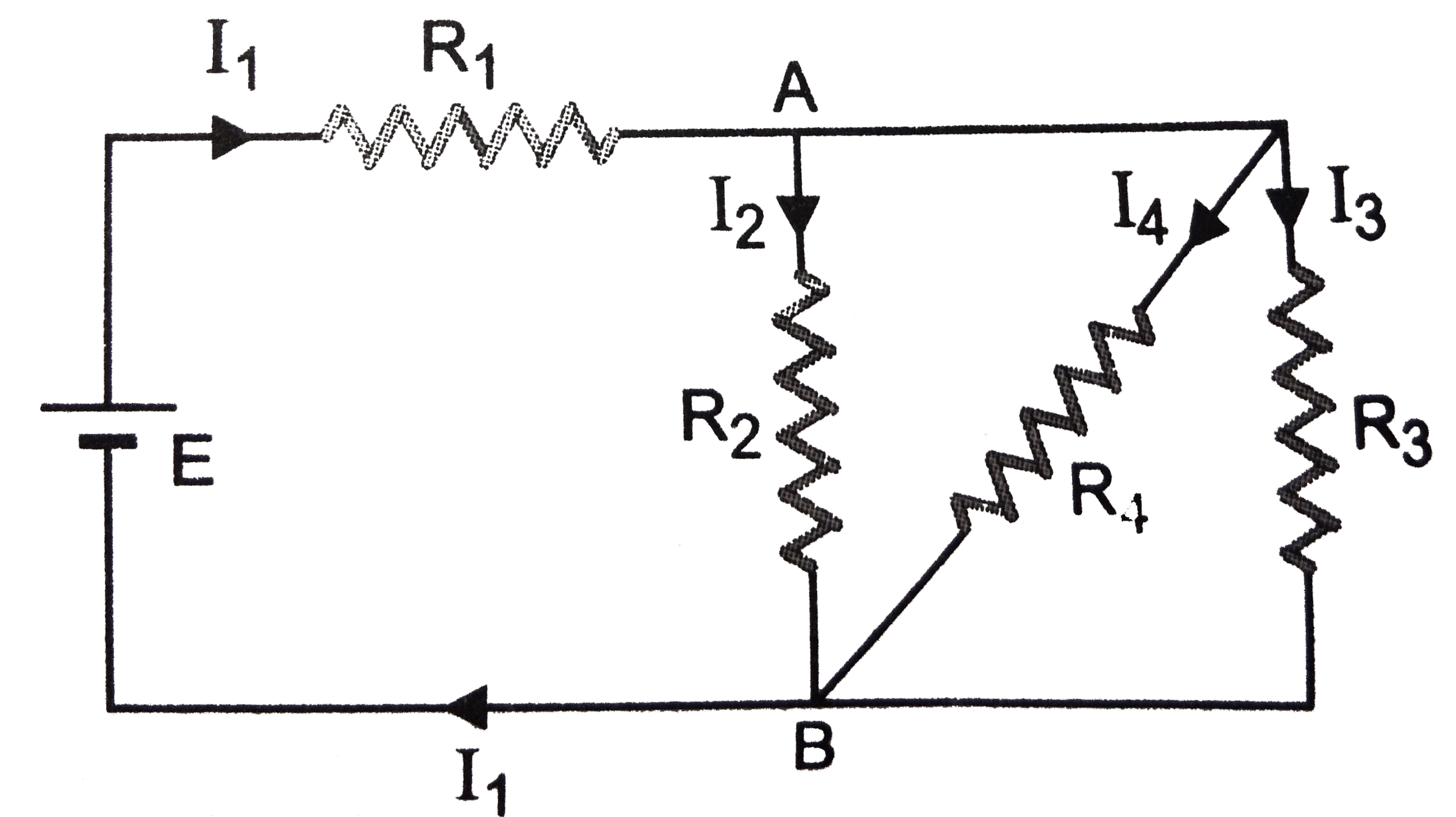
View SolutionIn the circuit R1=4Ω,R2=R3=15ΩR4=30ΩandE=10V Calculate the equivalent resistance of the circuit and current in each resistor
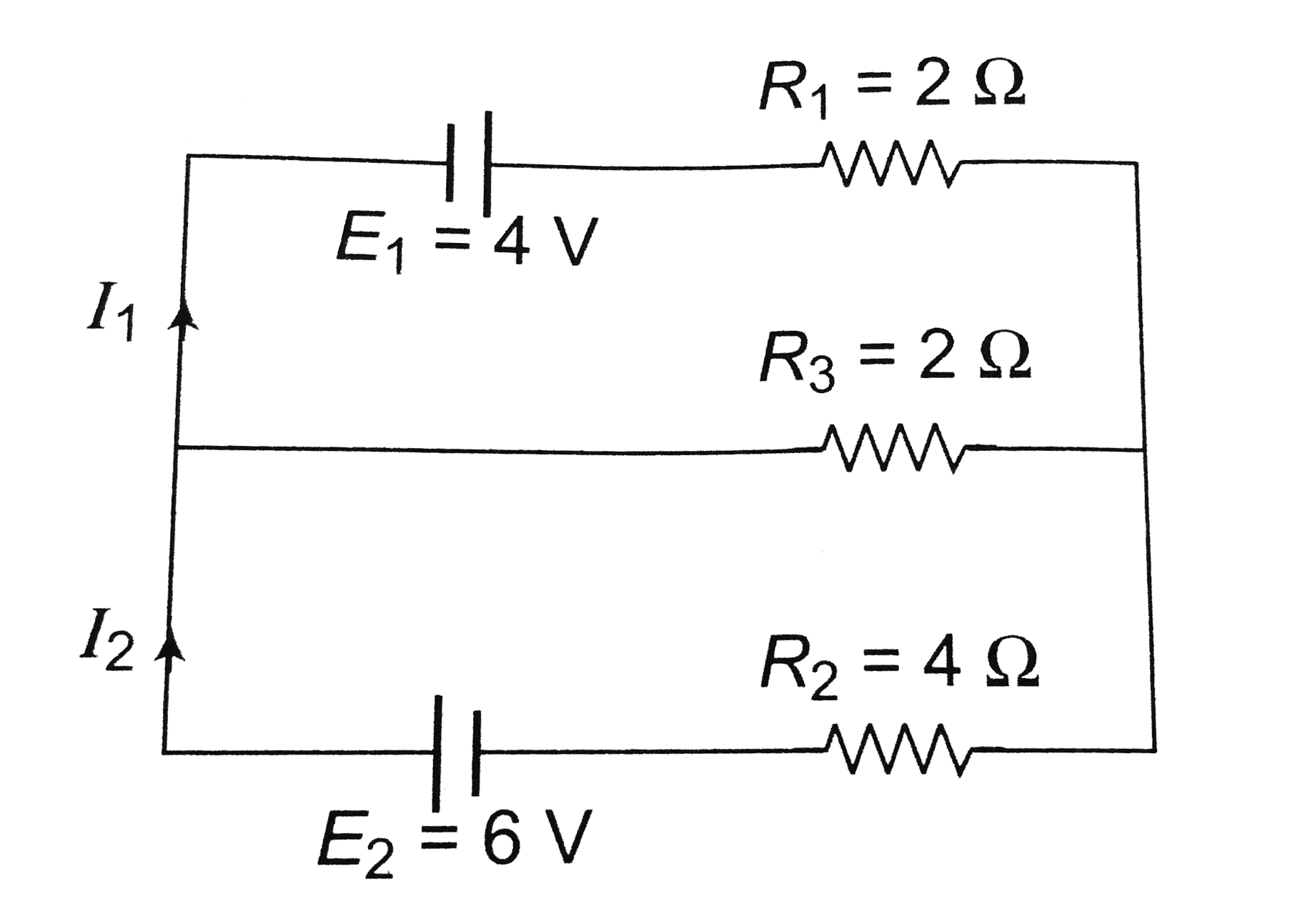
View SolutionIn the circuit shown below E1=4.0V,R1=2Ω,E2=6.0V,R2=4Ω and R3=2Ω. The current I1 is
View Solution
