Solv ethe equation |x−1|+|7−x|+2|x−2|=4Solution in Punjabi
Here critical points are 1,2,7 using the method of intervals, we find intervals when the expression x−1,7−x and x−2 are of constant signs.
i.e. x<1,1<x<2,2<x<7,x>7
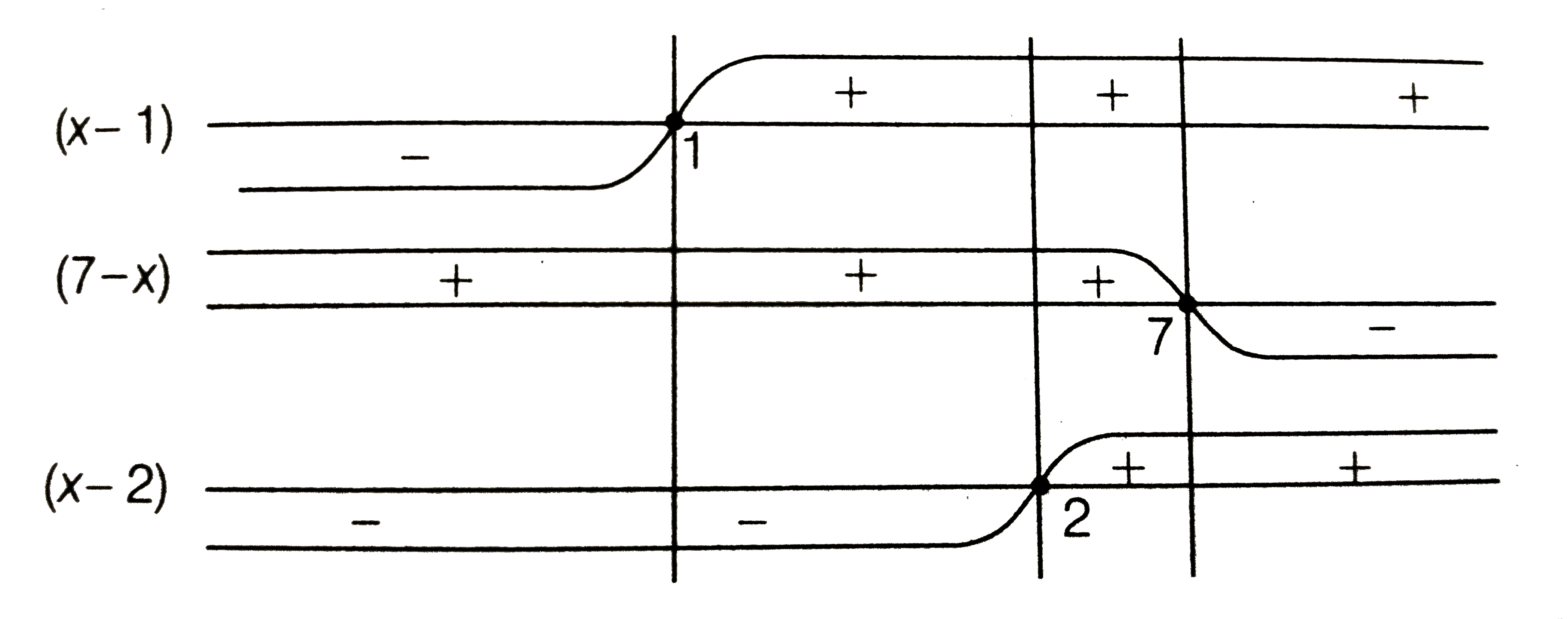
Thus, the given equation is equivalent to the collection of four systems,
⎡⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢
⎢⎣{x<1−(x−1)+(7−x)−2(x−2)=4{1≤x<2(x−1)+(7−x)−2(x−2)=4{2≤x<7(x−1)+(7−x)+2(x−2)=4{x≥7(x−1)−(7−x)+2(x−2)=4implies[({(xlt1),(x=2):}),({(1lexlt2),(x=3):}),({(2lexlt7),(x=1):}),({(xge7),(x=4):}):}
From the collection of four systems, the given equation has no solution.
Topper's Solved these Questions
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 1
11 Videos
- THEORY OF EQUATIONSBOOK - ARIHANT MATHSCHAPTER - THEORY OF EQUATIONSEXERCISE - Exercise For Session 2
10 Videos
- THE STRAIGHT LINESBOOK - ARIHANT MATHSCHAPTER - THE STRAIGHT LINESEXERCISE - The Straight Lines Exercise 8 : (Questions Asked in Previous 13 years Exams)
1 Videos
- THREE DIMENSIONAL COORDINATE SYSTEMBOOK - ARIHANT MATHSCHAPTER - THREE DIMENSIONAL COORDINATE SYSTEMEXERCISE - Three Dimensional Coordinate System Exercise 12 : Question Asked in Previous Years Exam
2 Videos
Similar Questions
If (a2−1)x2+(a−1)x+a2−4a+3=0 is identity in x , then find the value of a .
View SolutionIf α and β are the roots of the equation 2x2−3x+4=0, then the equation whose roots are α2 and β2, is a. 4x2+7x+16=0 b. 4x2+7x+6=0 c. 4x2+7x+1=0 d. 4x2−7x+16=0
View SolutionSolve the following system of inequalities graphically
x+5y≤25,2x+2y≥2,2x−2y≤0,x≥0,y≥0
View SolutionConsider the line L1:x−12=y−1=z+31,L2:x−41=y+31=z+32 find the angle between them.
View SolutionSolve the following equations: log_(7)(2^(x)-1)+log_(7)(2^(x)-7)=1
View SolutionSolve: (4+x)(5−x)(2+x)(7−x)=1
View Solutionसमीकरण 1x+1+2x+2=4x+4x≠−1,−2,−4 को हल कीजिए।
View SolutionSolve : (x−4)(x−7)(x−2)(x+1)=16
View Solutionइन समीकरण को हल कीजिये tan−1x−2x−4+tan−1x+2x+4=π4
View SolutionSolve the equation 2(x+2)−3(x−3)=x+7
View Solutionதீர்க்க : (x−4)(x−7)(x−2)(x+1)=16
View SolutionSolve the equation. x−2=7
View SolutionSolve: (4+x)(5−x)(2+x)(7−x)=1
View SolutionSolve the equation
|x+2|+|x+5|=7
View SolutionSolve the following equations : 15(x−1)+4(x+3)=2(7+x)
View SolutionSolve: (x-4) (x-7) (x-2) (x+1)=16
View Solution
