Solve (a) tanx<2 cosx≤−12Solution in Tamil
The correct Answer is:(a) ∪n∈Z(nπ−π2,nπ+tan−12)
(b) ∪n∈Z[2nπ+2π3,2nπ+4π3]
(a) We know that tanx is periodic with period π. So, check the solution in the interval (−π2,π2).
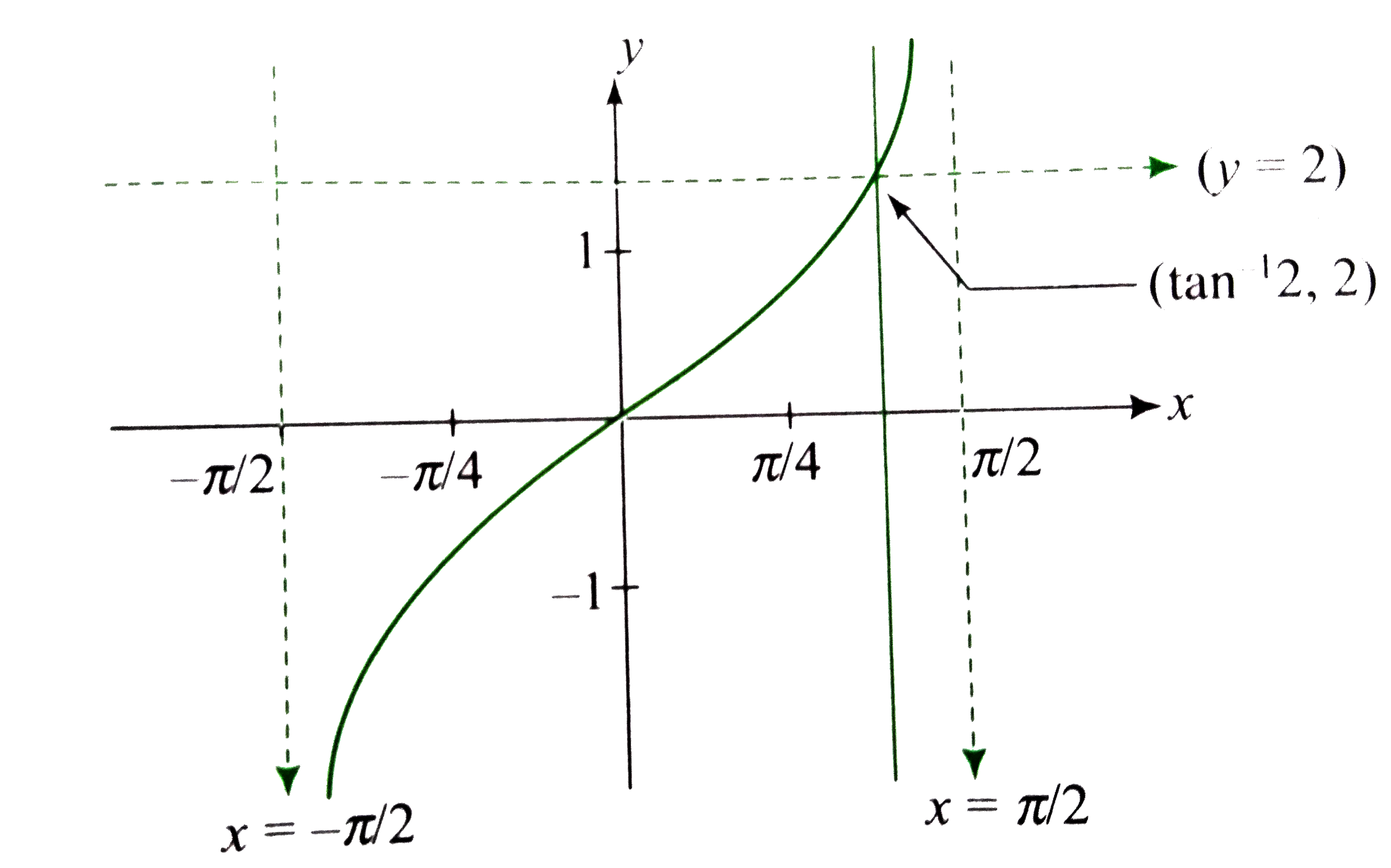
It is clear from the figure that tanx<2 when
−π2<x<tan−12.
Therefore, general solution is
∪n∈Z(nπ−π2,nπ+tan−12)
(b) cosx is periodic with period 2π.
So, check the solution in [0,2π].

It is clear from the figure that cosx≤−12 when
2π3≤x≤4π3.
On generalizing the above solution, we get
x∈∪n∈Z[2nπ+2π3,2nπ+4π3]
Topper's Solved these Questions
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.7
5 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.8
9 Videos
- RELATIONS AND FUNCTIONSBOOK - CENGAGECHAPTER - RELATIONS AND FUNCTIONSEXERCISE - Exercise 1.5
5 Videos
- Quadratic Equations, Inequalities, Modulus and LogarithmsBOOK - CENGAGECHAPTER - Quadratic Equations, Inequalities, Modulus and LogarithmsEXERCISE - Question Bank
28 Videos
- SCALER TRIPLE PRODUCTS BOOK - CENGAGECHAPTER - SCALER TRIPLE PRODUCTS EXERCISE - DPP 2.3
11 Videos
Similar Questions
Find the domain of the following following functions:
(a) f(x)=sin−1x
(b) f(x)=sin−1(|x−1|−2)
(c ) f(x)=cos−1(1+3x+2x2)
(d ) f(x)=sin−1(x−3)√9−x2
(e ) f(x)=cos−1(6−3x4)+cosec−1(x−12)
(f) f(x)= ⎷sec−1(2−|x|4)
View SolutionFind the domain of the function : f(x)=√4x+8(23)(2x−2)−13−22(x−1)
View SolutionThe entire graph of the equation y=x2+kx−x+9 in strictly above the x−aξs if and only if k<7 (b) −5<k<7 k≻5 (d) none of these
View SolutionLet a,b,c,d be positive integers such that (log)ab=32and(log)cd=54. If (a−c)=9, then find the value of (b−d).
View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj+ˆk and ˆi−ˆj+ˆk, in the order from right-handed system ∀x ∈R, is
View SolutionSolve :(tanx−1√3)(cosx−12)≤0.
View Solutionनिम्नलिखित समाकलों को हल कीजिए ।
∫1cos2x.(1−tanx)2dx
View Solutionहल करें tanx+cotx=2
View SolutionSolve the equation, (1−tanx)(1+sin2x)=1+tanx
View SolutionSolve the equation 1+tanx1−tanx=1+sin2xcos2x.
View Solutionসমাধান করোtanx+cotx=2
View SolutionSolve (log)tanx(2+4cos2x)=2
View SolutionSolve (log)tanx(2+4cos2x)=2
View Solution∫.sec2xdx(1+tanx)(2+tanx) को हल कीजिए।
View Solutionint(sec^2 xdx)/((1+tanx)(2+tan x)) Solve
View SolutionSolve secx−1=(√2−1)tanx
View Solution
