Solve for x and y, by reducing the following equations in a pair of linear equations :
2x + 3y = 5xy and 3x - 2y = xy.
To solve the equations 2x+3y=5xy and 3x−2y=xy, we will follow these steps:
Step 1: Rewrite the equations
We start with the two equations:
1. 2x+3y=5xy
2. 3x−2y=xy
Step 2: Rearranging the equations
We can rearrange both equations to isolate terms involving xy:
1. 5xy−2x−3y=0
2. xy−3x+2y=0
Step 3: Divide both equations by xy
To reduce these equations into a simpler form, we divide both equations by xy:
1. 2xxy+3yxy=5 simplifies to 2y+3x=5 (let's call this Equation 3).
2. 3xxy−2yxy=1 simplifies to 3y−2x=1 (let's call this Equation 4).
Step 4: Substitute u and v
Let u=1x and v=1y. Then we can rewrite the equations:
1. From Equation 3: 2v+3u=5 (Equation 5).
2. From Equation 4: 3v−2u=1 (Equation 6).
Step 5: Solve the linear equations
Now we have a pair of linear equations:
1. 2v+3u=5
2. 3v−2u=1
To eliminate u, we can multiply Equation 5 by 2 and Equation 6 by 3:
1. 4v+6u=10 (Equation 7).
2. 9v−6u=3 (Equation 8).
Step 6: Add the equations
Now, we add Equation 7 and Equation 8:
(4v+6u)+(9v−6u)=10+3
This simplifies to:
13v=13⟹v=1
Step 7: Substitute back to find u
Now substituting v=1 back into Equation 5:
2(1)+3u=5⟹2+3u=5⟹3u=3⟹u=1
Step 8: Find x and y
Since u=1x and v=1y:
1. u=1⟹x=1
2. v=1⟹y=1
Final Solution
Thus, the solution for the equations is:
x=1,y=1
We start with the two equations:
1. 2x+3y=5xy
2. 3x−2y=xy
We can rearrange both equations to isolate terms involving xy:
1. 5xy−2x−3y=0
2. xy−3x+2y=0
To reduce these equations into a simpler form, we divide both equations by xy:
1. 2xxy+3yxy=5 simplifies to 2y+3x=5 (let's call this Equation 3).
2. 3xxy−2yxy=1 simplifies to 3y−2x=1 (let's call this Equation 4).
Let u=1x and v=1y. Then we can rewrite the equations:
1. From Equation 3: 2v+3u=5 (Equation 5).
2. From Equation 4: 3v−2u=1 (Equation 6).
Now we have a pair of linear equations:
1. 2v+3u=5
2. 3v−2u=1
1. 4v+6u=10 (Equation 7).
2. 9v−6u=3 (Equation 8).
Now, we add Equation 7 and Equation 8:
(4v+6u)+(9v−6u)=10+3
This simplifies to:
13v=13⟹v=1
Now substituting v=1 back into Equation 5:
2(1)+3u=5⟹2+3u=5⟹3u=3⟹u=1
Since u=1x and v=1y:
1. u=1⟹x=1
2. v=1⟹y=1
Thus, the solution for the equations is:
x=1,y=1
Topper's Solved these Questions
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3a
18 Videos
- LINEAR EQUATIONS IN TWO VARIABLES BOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLES EXERCISE - Exercise 3A
8 Videos
- INTRODUCTION TO TRIGONOMETRYBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - INTRODUCTION TO TRIGONOMETRYEXERCISE - Revision Exercise Long Answer Questions
5 Videos
- POLYNOMIALSBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - POLYNOMIALSEXERCISE - Revision Exercise Long Answer Questions
4 Videos
Similar Questions
Knowledge Check
Which of the following is the graph of the equation y = 2x − 5 in the xy-plane?
A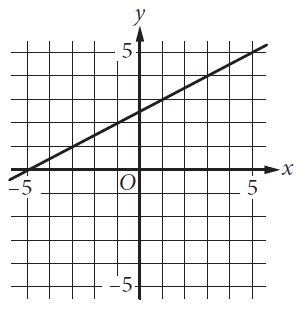 B
B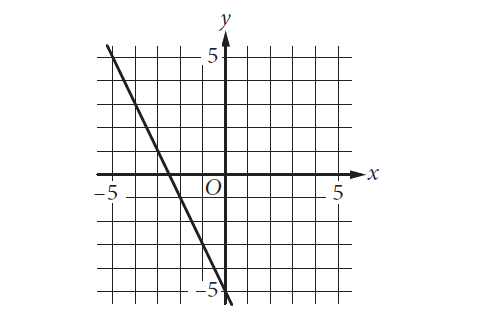 C
C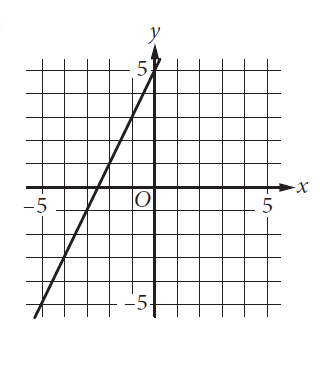 D
D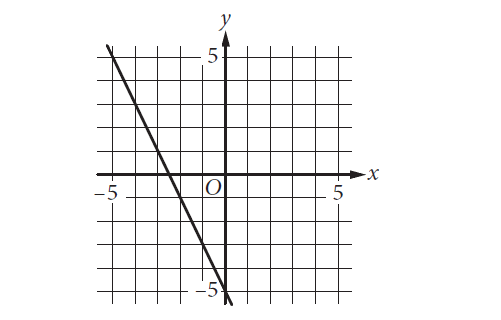
Examine whether the following equation represents a circle or not : 3x2+3y2+2xy+3x+y=0
View SolutionSolve the pair of equations : 2x+3y=13,5x−4y=−2
View SolutionSolve the following system of linear equations by matrix method: 3x−2y=7,5x+3y=1
View SolutionSolve the following pairs of equations by reducing them to a pair of linear equations:(i) 12x+13y=2; 13x+12y=136 (ii) 2√x+3√y=2; 4√x−9√y=−1(iii) 4x+3y=14; 3x−4y=23
View SolutionSolve the following pair of equations by reducing them to a pair of linear equations:5x−1+1y−2=26x−1−3y−2=1
View SolutionSolve the following system of linear equations by Cramers rule: 2x−y=17, 3x+5y=6
View SolutionSolve the following system of linear equations by Cramers rule: 2x−y=−2, 3x+4y=3
View Solution
