Solve, √x−6−√10−x≥1.
Video Solution
Text Solution
The correct Answer is:x∈[(16+√7)/2,10]
We have√x−6−√10−x≥1
We must have x≥6 and x≤10
Then √x−6≥1+√10−x
Squaring given inequality,
x−6≥1+10−x+2√10−x
⇒2x−17≥2√10−x
Clearly LHS must be positive.
∴x≥172
So we have
4x2+289−68x≥4(10−x)
⇒4x2−64x+249≥0
⇒x2−16x+2494≥0
⇒(x−8)2−(√72)2≥0
⇒(x−8−√72)(x−8+√72)≥0
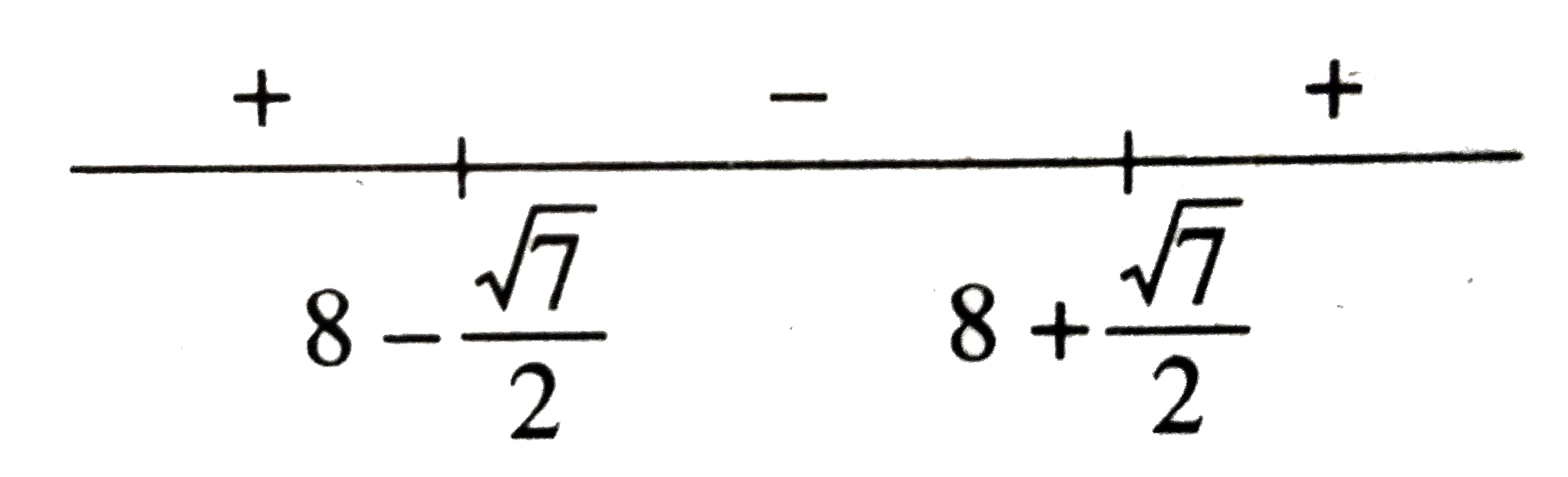
From the sign scheme, x∈[(16+√7)/2,10]
|
Topper's Solved these Questions
- INEQUALITIES AND MODULUSBook:CENGAGEChapter:INEQUALITIES AND MODULUSExercise:Single correct Answer
Explore 21 Videos
- INDEFINITE INTEGRATIONBook:CENGAGEChapter:INDEFINITE INTEGRATIONExercise:Question Bank
Explore 25 Videos
- INEQUALITIES INVOLVING MEANS Book:CENGAGEChapter:INEQUALITIES INVOLVING MEANS Exercise:Exercise (Numerical) & JEE Previous Year
Explore 11 Videos
