Solve tanx>cotx, where x∈[0,2π].Solution in Tamil
Video Solution
Text Solution
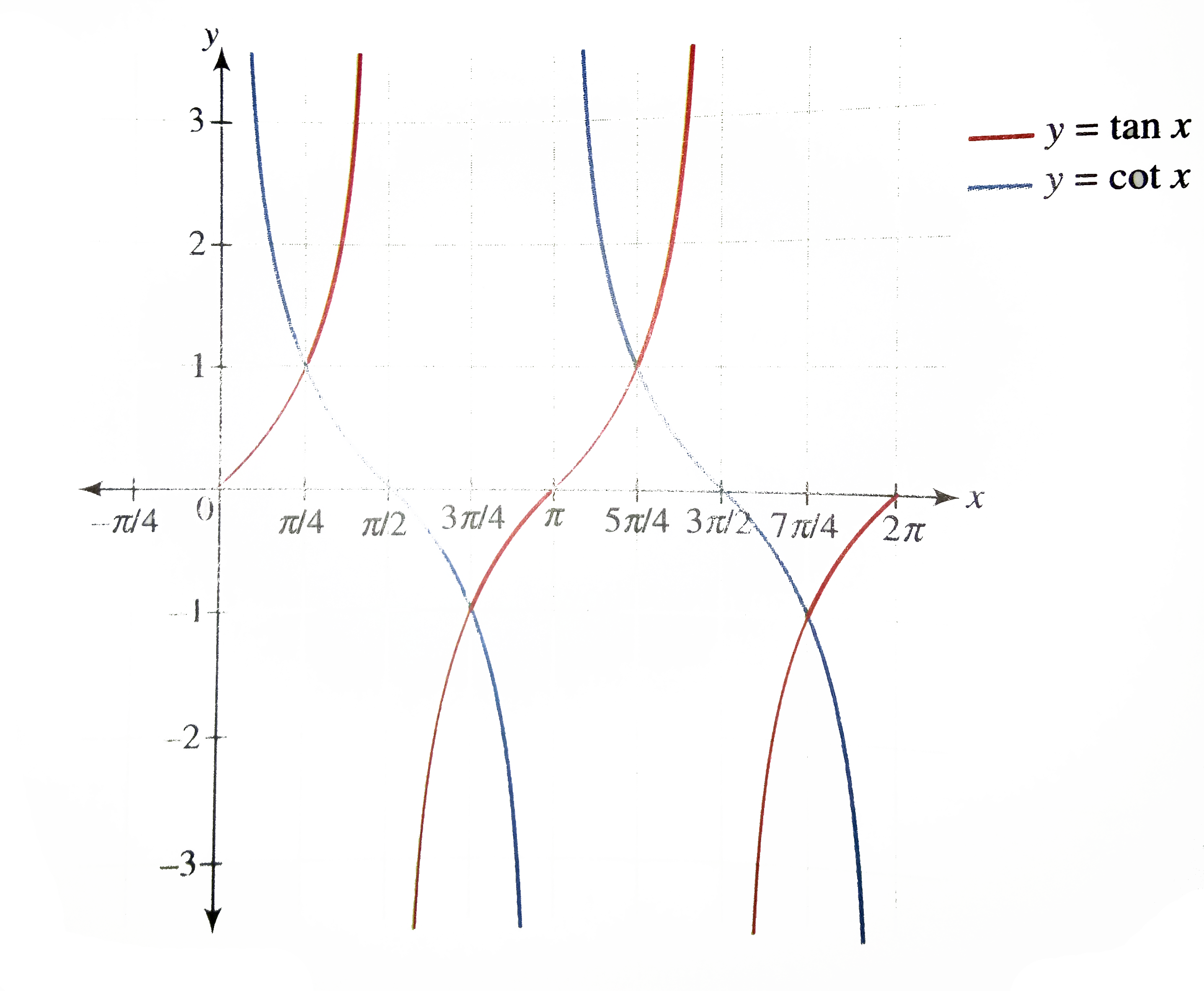
tanx>cotx
⇒ values of tanx are more than the values of cotx
⇒ values of x for which the graph of y=tanx is above the graph of y=cotx From the graph, it is clear that x∈(π/4,π/2)∪(3π/4,π)∪(5π/4,3π/2)∪(7π/4,2π).
|
Similar Questions
Solve tanx>cotx, where x∈[0,2π].
View SolutionSolve tanx>cotx, where x∈[0,2π].
View Solutiondifferentiate (tanx)cotx+(cotx)tanx
View SolutionLet f(x)=max{tanx, cotx}. Then the number of roots of the equation f(x)=1√3 in (0,2π) is
View Solutioncotxcotx−cot3x+tanxtanx−tan3x=
View Solutionddx[tanx−cotxtanx+cotx]=
View SolutionSolve |sinx+cosx|=|sinx|+|cosx|,x∈[0,2π].
View Solution
