Solve the following LPP graphically
Maximize, Z=5x1+3x2
Subject to 3x1+5x2≤15
5x1+2x2≤10
x1,x2≥0 Solution in Odia
The correct Answer is:Z(max) is 23519 at x1=2019andx2=4519
Step by step video, text & image solution for Solve the following LPP graphically Maximize, Z=5x_(1) +3x_(2) Subject to 3x_(1)+5x_(2) le 15 5x_(1)+2x_(2) le 10 x_(1),x_(2) ge 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - ARIHANT PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Chapter Test (1 MARK Questions)
7 Videos
- LINEAR PROGRAMMINGBOOK - ARIHANT PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Chapter Test (4 MARKS Questions)
6 Videos
- LINEAR PROGRAMMINGBOOK - ARIHANT PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - PRACTICE QUESTIONS (Exams., Textbook.s & Other Imp. Questions) (4 Marks Questions)
9 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - ARIHANT PRAKASHANCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - Chapter Test (6 MARKS Questions)
3 Videos
- MATRICESBOOK - ARIHANT PRAKASHANCHAPTER - MATRICESEXERCISE - Chapter Test ( 6 Mark Questions)
4 Videos
Similar Questions
Draw the following convex polygons on the graph paper and indicate it by shading and mention the vertices.
x+y≤5,x+y≥2,x,y≥0
View SolutionFind the feasible region of x−2y≥0,3x−6y≤0,x,y≥0.
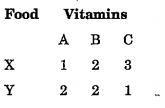
View SolutionTwo types of food X and Y re mixed to prepare a mixture is such a way that the mixture contains at least 10 units of vitamin A, 12 units of vitamin B and 8 units of vitamin X. These vitamines are avialalbe in 1kg of food as per table below. 1kg of food X costs Rs 16 and 1kg of food Y costs Rs 20. Formulate the L. P. P. so as to determine the least cost of the mixture containing the required amound of vitamins.
View SolutionIf sin−1(xa)+sin−1(yb)=αprove thatx2a2+2xyabcosα+y2b2=sin2α
View SolutionThere are two families A and B. There are 4 men, 6 women and 2 children in family A and 2 men, 2 women and 4 children in family B. The recommended daily amount of calories is 2400 for men, 1900 for women and 1800 for children, and 45 g of proteins for men, 55 g for women and 33 g for children. Represent the above information by matrices. Using matrices multiplication, calculate the total requirement of calories and proteins for each of the 2 families.
View SolutionIf the system of linear equations x_(1)+2x_(2)+3x_(3)=6,x_(1)+3x_(2)+5x_(3)=9,2x_(1)+5x_(2)+ax_(3)=b, is consistent and has infinite number of solutions,then :-
View Solutionनिम्न रैखिक समीकरण निकाय को लीजिये
x1+2x2+x3=3,2x1+3x2+x3=3,3x1+5x2+2x3=1 निकाय के-
View Solution5x1+3x2=30
5x1−2x2=5
View SolutionIf 3x1+5x2≤15,5x1+2x2≤10,x1,x2≥0, then the maximum value of z=5x1+3x2 by graphical method is
View SolutionBy graphical method, the solutions of linear programming problem maximise Z=3x1+5x2 subject to constraints 3x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 are
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
निम्नतम z=2x1+3x2
प्रतिबंध x1+x2≤4
6x1+2x2≥8
x1+5x2≥8
x1+5x2≥4
x1≤3
x2≤3
तथा x1,x2≥0
View Solutionआलेख विधि से निम्न रैखिक प्रोग्रामन समस्याओं को हल कीजिए -
अधिकतम z=3x1+2x2
प्रतिबंध x1+x2≥1
x2≡5x1≤0
5x2−x1≥0
x1−x2≤6
x1≤3
तथा x1≥0.x2≥0
View SolutionThe objective function Z=4x1+5x2, Subject to 2x1+x2≥7,2x1+3x2≤15,x2≤3,x1,x2≥0 has minimum value at the point
View Solutionनिम्न रैखिक समीकरण निकाय को लीजिये
x1+2x2+x3=3,2x1+3x2+x3=3,3x1+5x2+2x3=1 निकाय के-
View Solutionआलेखीय विधि से , रेखीय प्रक्रमन समस्या Z(अधितम)=3x1+5x23x1+2x2≤18,x1≤4,x2≤6x1≥0,x2≥0 का हल है
View SolutionThe solution of linear programming problem, maximize Z=3x1+5x2 subject to 3x1+2x2≤18,x1≤4,x2≤6,x1≥0,x2≥0 is ………..
View Solution
