Solve the following LPPs graphically.
maximise
Subject to
Solution in Odia
The correct Answer is:(3,0); max =15
Step by step video, text & image solution for Solve the following LPPs graphically. maximise Z = 5x_1 + 6x_2 Subject to 2x_1+3x_2 le 6 x_1,x_2 ge 0 by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- LINEAR PROGRAMMINGBOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - CHAPTER PRACTICE (Short Answer Type Questions 4 Marks)
11 Videos
- LINEAR PROGRAMMINGBOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - CHAPTER PRACTICE (Long Answer Type Questions 6 Marks)
18 Videos
- LINEAR PROGRAMMINGBOOK - ARIHANT PUBLICATIONCHAPTER - LINEAR PROGRAMMINGEXERCISE - ODISHA BUREAU.S TEXTBOOK SOLUTIONS (Exercise 3(a))
11 Videos
- INVERSE TRIGONOMETRIC FUNCTIONS BOOK - ARIHANT PUBLICATIONCHAPTER - INVERSE TRIGONOMETRIC FUNCTIONS EXERCISE - CHAPTER PRACTICE
35 Videos
- MATRICES BOOK - ARIHANT PUBLICATIONCHAPTER - MATRICES EXERCISE - CHAPTER PRACTICE (Very Short Answer Type Questions)
56 Videos
Similar Questions
Feasible region (shaded) for an LPP is shown in the following figure, Maximise Z = 5x + 7y
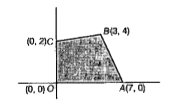
View SolutionFind the maximum and minimum value of 2x + y subjects to the constraints are
x+3y≥6,x−3y≤3,3x+4y≤24
−3x+2y≤6,5x+y≥5 and x,y≥0
View SolutionA merchant sells two models X and Y of TV with cost price ₹ 25000 and ₹ 50000 Per set respectively. He gets a profit of ₹ 1500 on model X and ₹ 2000 on model Y . The sales connot exceed 20 sets in a month. If he cannot invest more than 6 lakh rupees, formulate the problem of determining the number of sets of each type he must keep in stock for maximum profit.
View SolutionEvaluate cot−1(−√3).
View SolutionWhat possible orders of a matrix can have , if it has
(i) 5 elements ?
(ii) 8 elements ?
View SolutionThe minimum vlaue Z=2x1+3x2 subject to the conditions 2x1+7x2≥22,x1+x2≥6,5x1+x2≥10 and x1,x2≥0 is
View SolutionSolve the following LPP graphically : Maximize : Z=5x1+3x2 subject to : 3x1+5x2≤15 5x1+2x2≤10 x1,x2≥0
View SolutionSolve the following LPP graphically Optimize Z=5x1+25x2 subject to −0.5x1+x2≤2,x1+x2≥2,−x1+5x2≥5,x1,x2≥0
View SolutionMaximizeZ=5x1+6x2
Subject to:2x1+3x2≤6
x1,x2≥0
View SolutionMinimize:Z=6x1+7x2
Subject to:x1+2x2≥4
x1,x2≥0
View SolutionSolve the following LPP graphically Maximize z=5x1+3x2
Subject to 3x1+5x2≤15<br>,5x1+2x2≤10<br>,x1,x2≥0.
View SolutionSolve the following LPP graphically Optimize Z=5x1+25x2 subject to −0.5x1+x2≤2,x1+x2≥2,−x1+5x2≥5,x1,x2≥0
View SolutionSolve the following LPP graphically Maximize z=5x1+3x2
Subject to 3x1+5x2≤15<br>,5x1+2x2≤10<br>,x1,x2≥0.
View SolutionSolve the following LPP graphically.
Minimise Z=20x1+40x2
Subject to 36x1+6x2≥1083x1+12x2≥36
2x1+x2≥10,x1,x2≥0
View SolutionSolve the following LPP graphically
Maximise Z=20x1+10x2
Subject to x1+2x2≤40
3x1+x2≥30,4x1+3x2≥60,x1≥0,x2≥0
View Solution
