Solve the following problem graphically :
Minimise and Maximise Z=3x+9y . . . (1)
subject to the constraints: x+3y≤60 . . . (2)
x+y≥10 . . . (3)
x≤y . . . (4)
x≥0,y≥0 . . . (5)
Region represented by x+3y≤60
Consider the equation x+3y=60.
x=0⇒3y=60⇒y=20,y=0⇒x=60
Plot the points A(2,20)andB(60,0). Join AB and produce it both ways.
Putting x=0andy=0. we get 0+3×0=0≤60.
∴O(0,0) line in the region x+3y≤60.
So, the region containing the origin is the solution set of x+3y≥60.
Region represented by x+y≥10
Consider the equation x+y=10.
Plot the points C(0,10)andD(10,0) Join CD and porducte it both ways.
Now, x=0,y=0⇒0+0≥10 is not true.
∴O(0,0) lies in the region x−y≤0.
We know that:
x≥0 is the y-axis and the region on its RHS.
y≥0 is the x-axis and the region above the x-axis.
On solving x=yandx+y=10, we get the point G(5,5).
On solving x=yandx+3y=60, we get H(15,15).
Thus, the feasible region is ACGH, as shown in the figure.
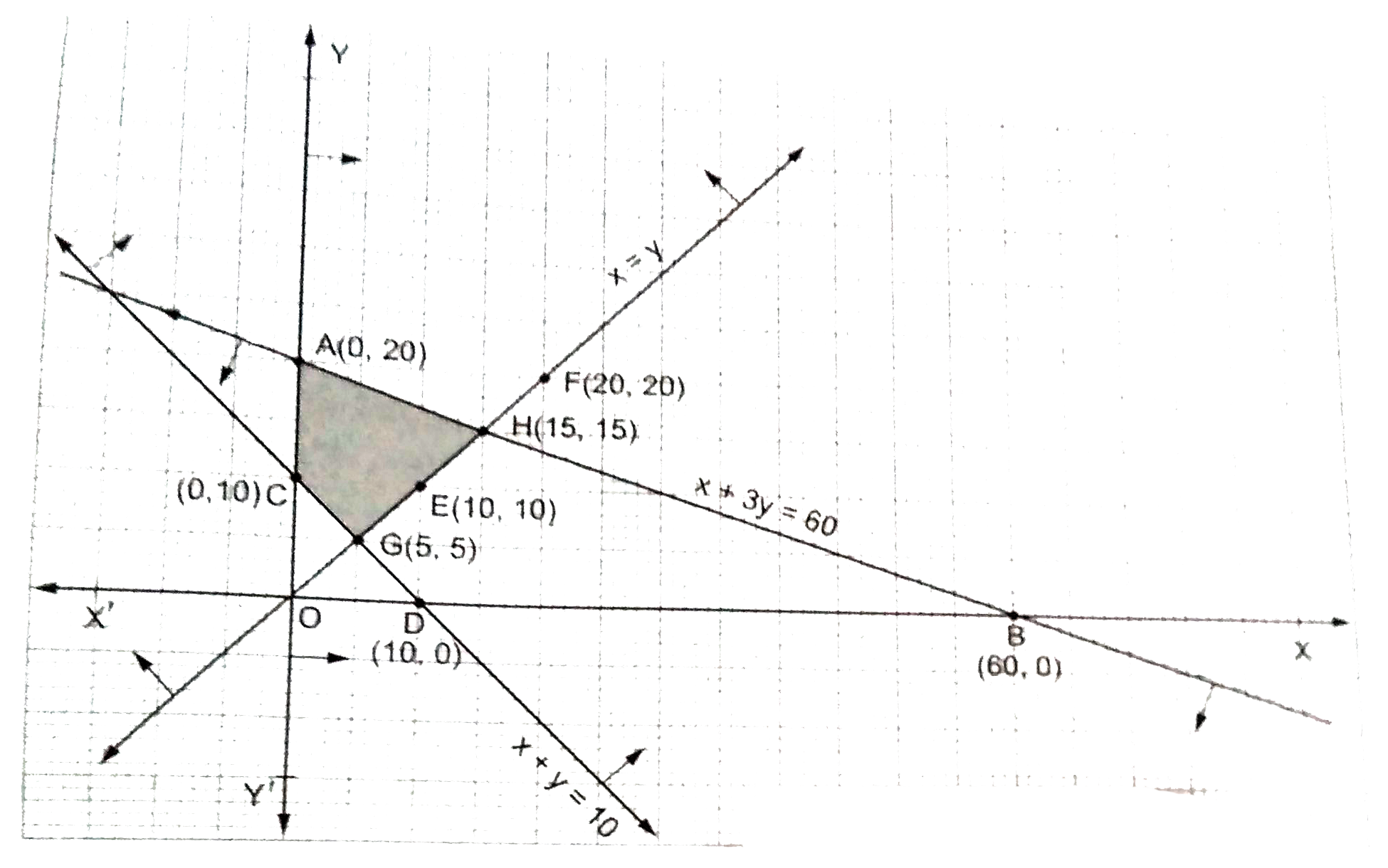
Value of z=3x+9y:
(i)AtA(0,20)itis(3×0+9×20)=180.
(ii)AtC(0,10)it is(3×0+9×10)=90.
(iii)AtC(5,5)it is(3×5+9×10)=60.
(iii)AtH(15,15)it is(3×15+9×15)=180.
So the minimum vlaue of z is 60 and its maximum value is 180.
Topper's Solved these Questions
- LINEAR PROGRAMMINGBook:RS AGGARWALChapter:LINEAR PROGRAMMINGExercise:Exprcise 33A
Explore 11 Videos
- LINEAR PROGRAMMINGBook:RS AGGARWALChapter:LINEAR PROGRAMMINGExercise:Exprcise 33B
Explore 38 Videos
- LINEAR DIFFERENTIAL EQUATIONS Book:RS AGGARWALChapter:LINEAR DIFFERENTIAL EQUATIONS Exercise:Objective Questions
Explore 27 Videos
- MATRICESBook:RS AGGARWALChapter:MATRICESExercise:Exercise 5F
Explore 21 Videos
Similar Questions
Knowledge Check
Solve the following linear programming problem graphically :Minimise Z=200x+500y. . . (1)subject to the constraints:x+2y≥10 . . .(2)3x+4y≤24 . . .(3)x≥0,y≥0 . . .(4)
A(Z)=(4,3)=2300B(Z)=(5,4)=2400C(Z)=(6,2)=2500D(Z)=(5,3)=2550Solve the Following Linear Programming Problem graphically : Maximise Z=3x+4ysubject to the constraints : x+y≤4,x≥0,y≥0.
A14B15C16D17
Solve the following problem graphically: Minimise and Maximise z = 2x + 6y Subject to the constraints: x+2y≤10, x+y≤7, x≥2, x≥0, y≥0
View SolutionSolve the following L.P.P graphically
Minimise and maximise z = 3x + 9y
Subject to the constraints x+3y≤60
x+y≥10
x≤y
x≥0,y≥0
View SolutionSolve the following problem graphically,Maximise and minimise z=5x+10y, subject to the constraints x+2y≤120,x+y≥60,−2y≥0andx,y≥0.
View SolutionSolve the following linear programming problem graphically: Maximise Z=4x+y . . . (1) , subject to the constraints:x+y≤50 . . .(2), 3x+y≤90 . . .(3) , x≥0,y≥0 . . .(4)
View SolutionMaximise z = 8x + 9y subject to the constraints given below : 2x+3y≤6 3x2y≤6 y≤1 x,y≥0
View SolutionMaximise Z=3x+4y
Subject to the constraints
x+y≤4,x≥0,y≥0
View Solution