Solve the following quadratic equation by factorisation.
(xi) 7m2=21m.Solution in Marathi
The correct Answer is:0, 3
Step by step video, text & image solution for Solve the following quadratic equation by factorisation. (xi) 7m^2=21m. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- QUADRATIC EQUATIONSBOOK - BAL BHARTICHAPTER - QUADRATIC EQUATIONSEXERCISE - Practice Set 2.3
6 Videos
- QUADRATIC EQUATIONSBOOK - BAL BHARTICHAPTER - QUADRATIC EQUATIONSEXERCISE - Practice Set 2.4
10 Videos
- QUADRATIC EQUATIONSBOOK - BAL BHARTICHAPTER - QUADRATIC EQUATIONSEXERCISE - Practice Set 2.1
17 Videos
- PYTHAGORAS THEOREM BOOK - BAL BHARTICHAPTER - PYTHAGORAS THEOREM EXERCISE - PRACTICE SET 2
27 Videos
- SIMILARITY BOOK - BAL BHARTICHAPTER - SIMILARITY EXERCISE - PROBLEM SET 1
12 Videos
Similar Questions
Solve the following quadratic equation by completing the square method.
(4) 9y2−12y+2=0
View SolutionCompare the given quadratic equation to the general form and write values of a, b, c: x2−7x+5=0
View SolutionWrite any two quadratic equations.
View SolutionWhich of the following is a Pythagorean triplet?
View SolutionIn ΔABCandΔPQR, in a one to one correspondence.
ABQR=BCPR=CAPQ, then
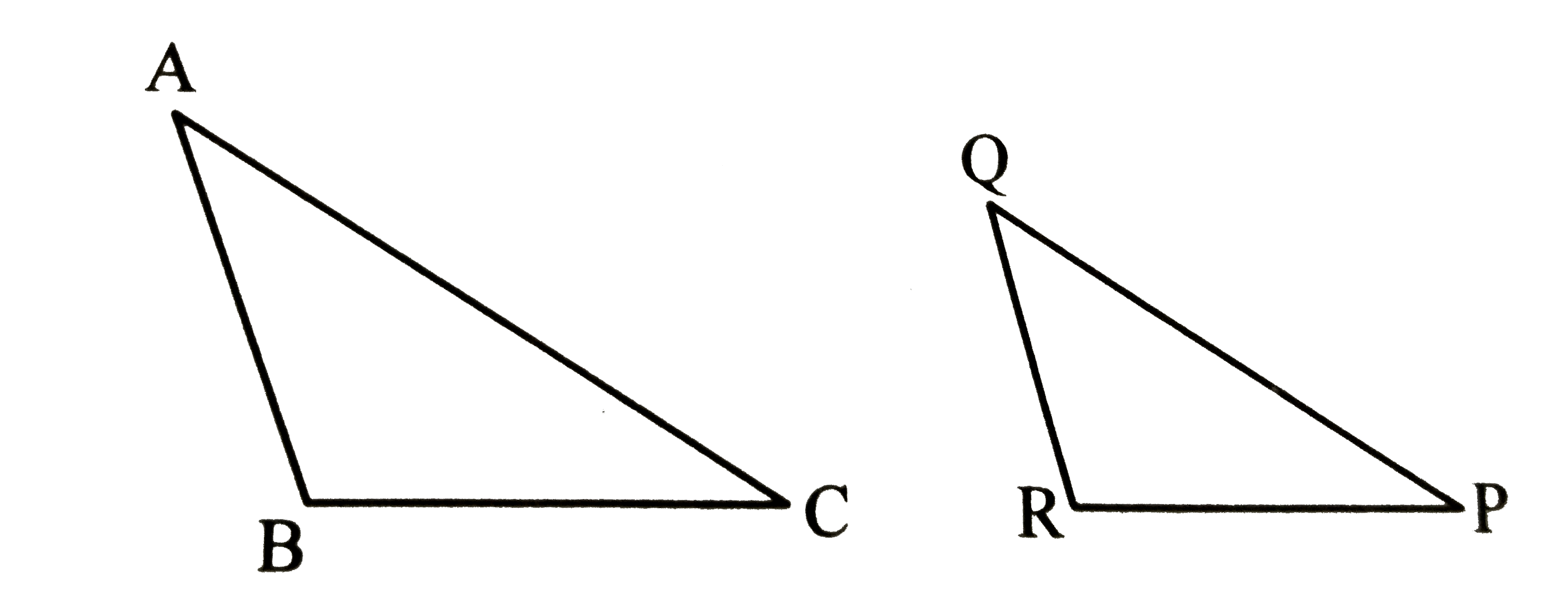
View Solution"21m^(2)-:7m
View SolutionSolve the following quadratic equation by factorisation method:
(xi) t2−49=0.
View SolutionSolve the following quadratic equations by factorisation method :
7y=−3y2−4
View SolutionSolve the following quadratic equations by factorization.
7m2=21m
View SolutionSolve the following quadratic equation by factorisation.
(xii) m2−11=0.
View SolutionSolve the following quadratic equation by factorisation method:
(viii) 3y2=15y.
View SolutionSolve the following quadratic equation by factorisation method:
(ix) x2=3
View SolutionSolve the following quadratic equation by factorization: 7m2=21m.
View SolutionSolve the following quadratic equations by factorization.
7m2=21m
View SolutionSolve the following quadratic equation by factorisation method:
(xi) t2−49=0.
View SolutionSolve the following quadratic equation by the method of factorisation:(xi)5x2−172x+32
View Solution
