Solve ∣∣x2−1∣∣+∣∣x2−4∣∣<6 graphically.

Video Solution
Doubtnut Promotions Banner
Text Solution
Verified by Experts

We have ∣∣x2−1∣∣+∣∣x2−4∣∣<6
∵∣∣x2−1∣∣<6−∣∣x2−4∣∣
Let us draw the graphs of y=∣∣x2−1∣∣andy=6−∣∣x2−4∣∣.
The graph of y=∣∣x2−1∣∣ is as follows.
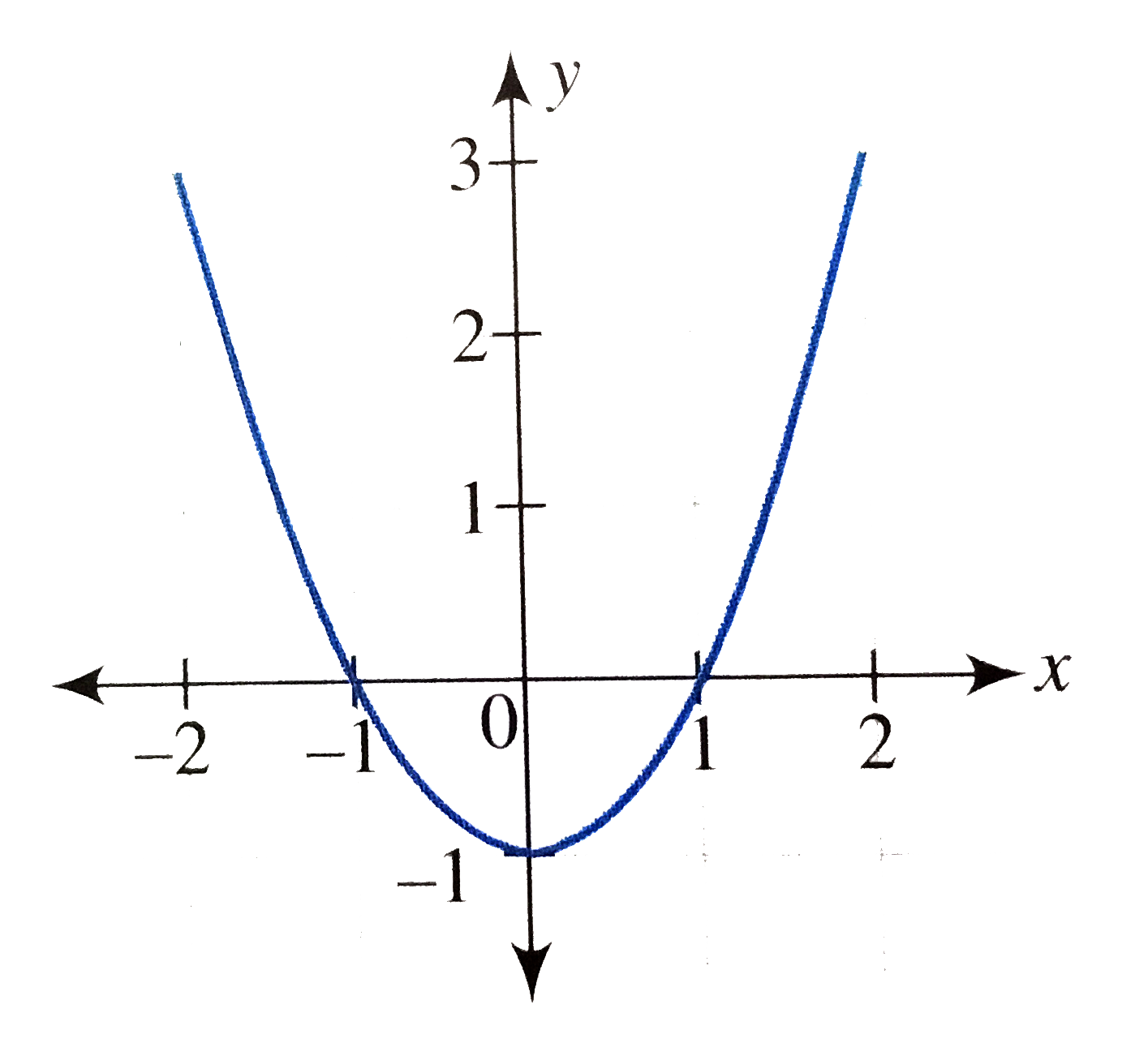
ocr_image
Graph of y=∣∣x2−1∣∣ is as follows.
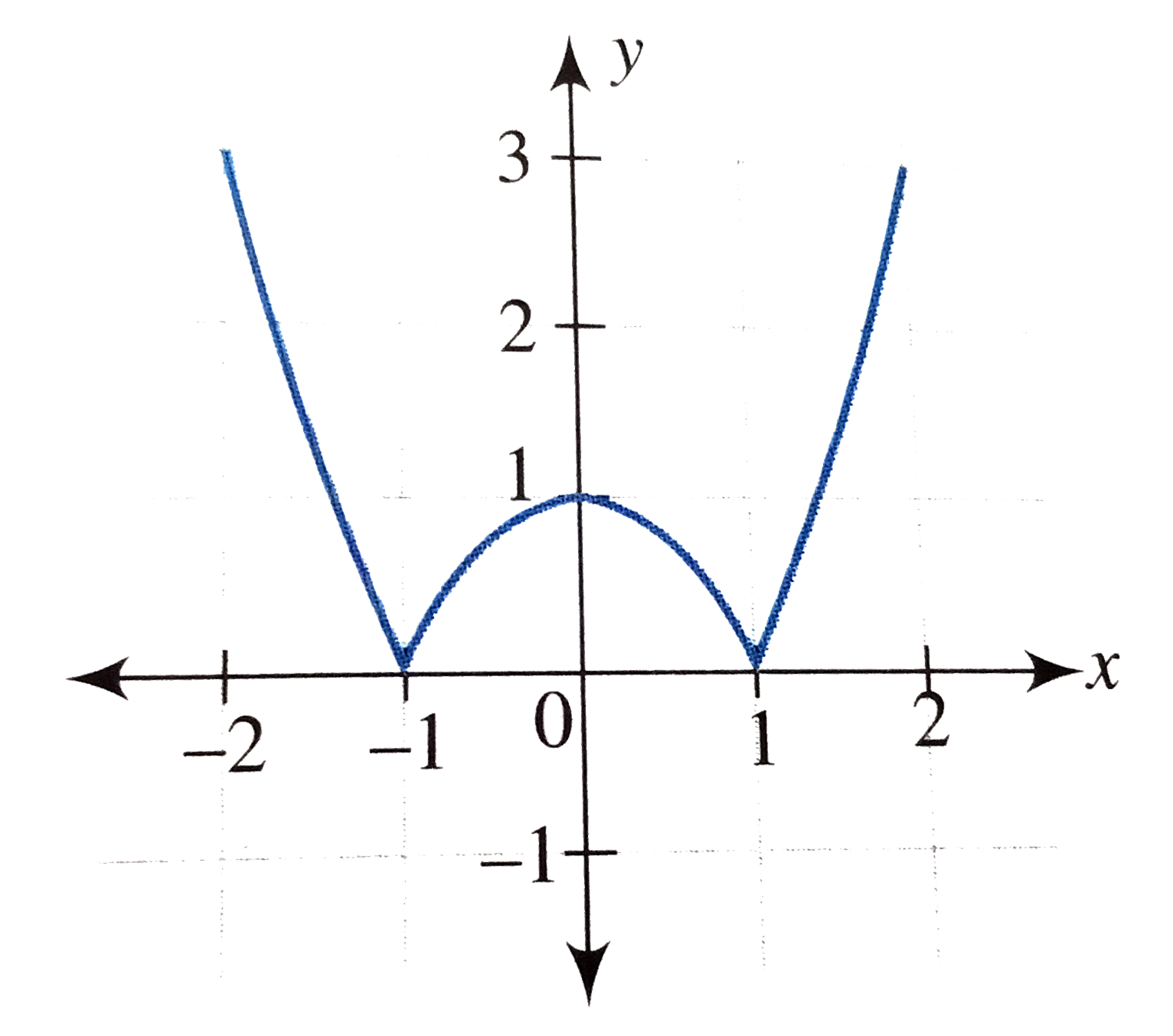
ocr_image
Graph of y=∣∣x2−4∣∣ is as follows.
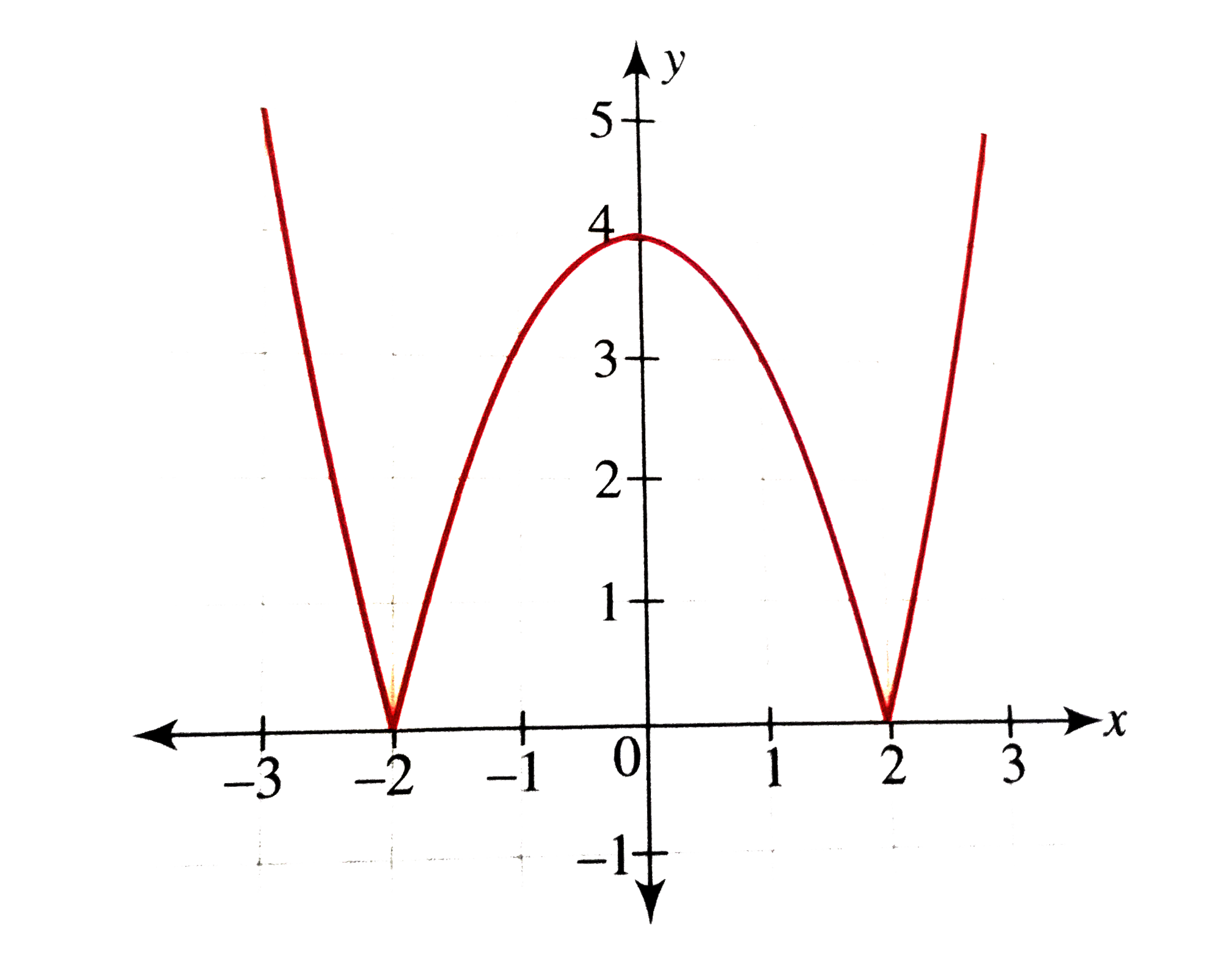
ocr_image
Garph of y=∣∣x2−4∣∣ is as follows 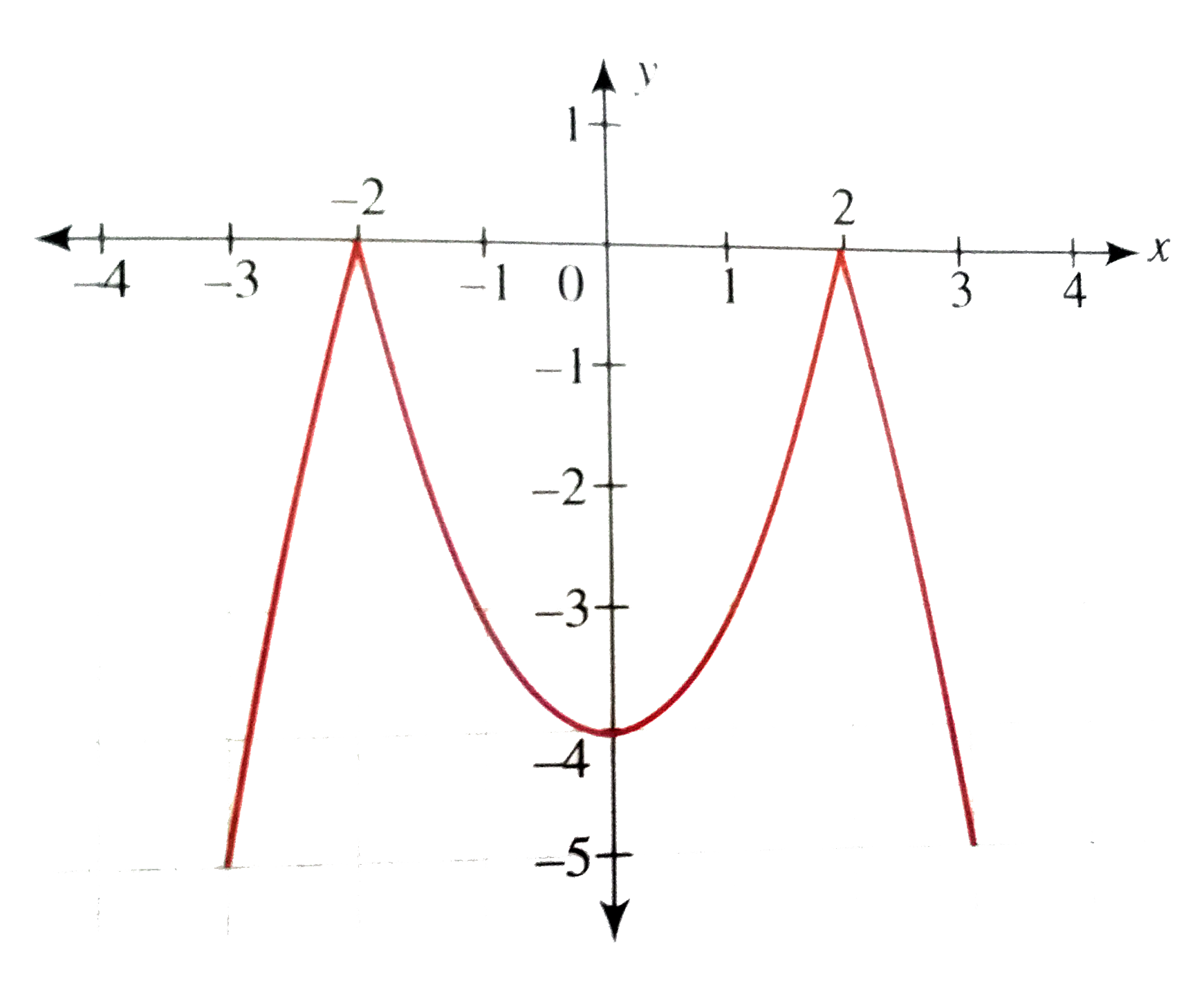ocr_image
Graph of y=6−∣∣x2−4∣∣ is as follows.
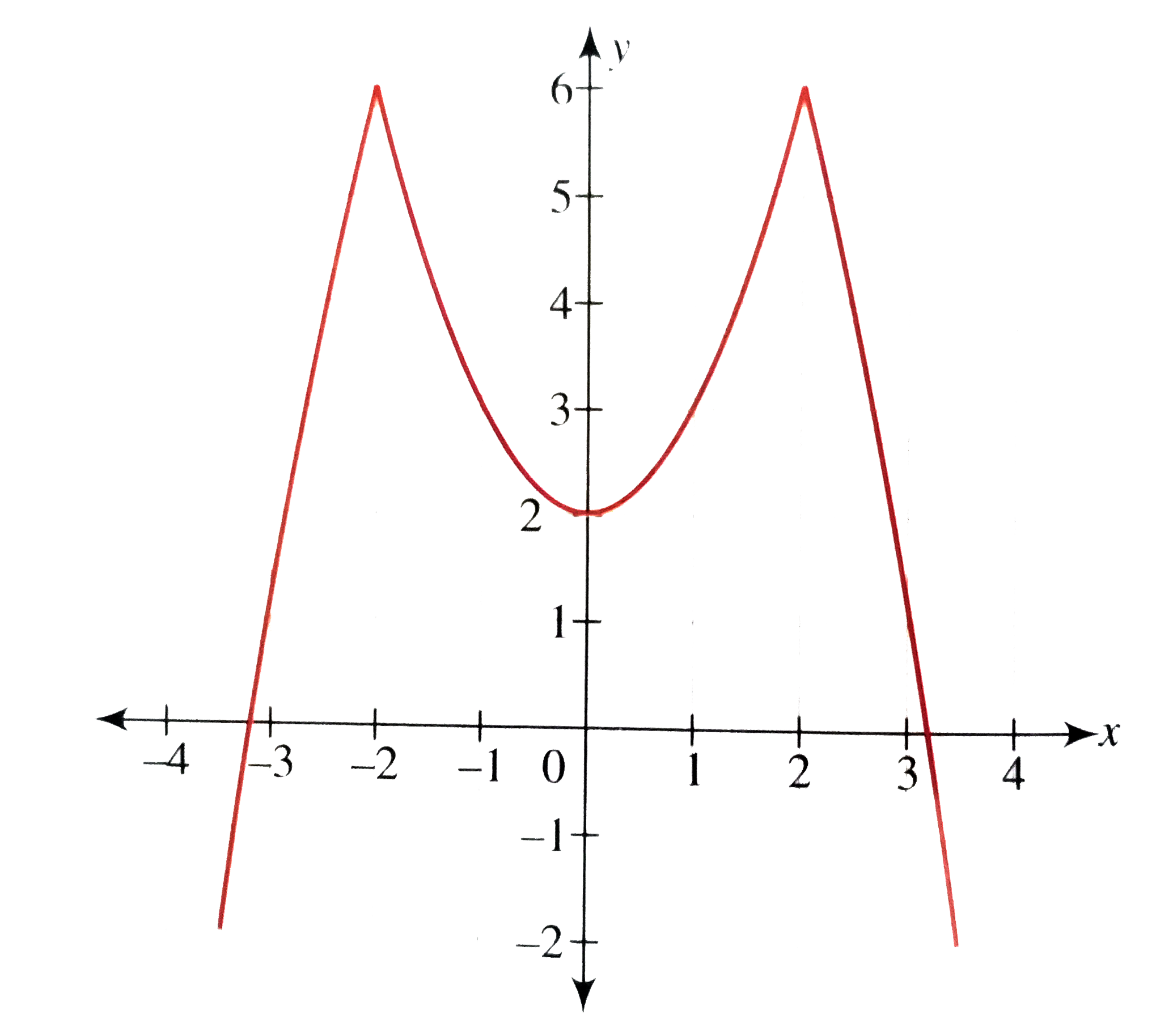
ocr_image
Graphs of y=∣∣x2−1∣∣andy=6−∣∣x2−4∣∣ are as shown in the following figure.
ocr_image
For ∣∣x2−1∣∣<6−∣∣x2−4∣∣, the graph of y=∣∣x2−1∣∣ lies below the graph of y=6−∣∣x2−4∣∣, the values of x lying between points A and B.
Solving y=∣∣x2−1∣∣andy=6−∣∣x2−4∣∣ for points of intersection, we have x2−1=6−(x2−4)orx2=11/2.
From the graph, the solution is x∈(−√112,√112).

Updated on:21/07/2023
|