Solve x2−4−[x]=0 (where [] denotes the greatest integer function).Solution in Bengali
We have x2−4−[x]=0
or x2−4=[x]
To, solve the equation we first locate the roots, for which we draw the graphs of y=x2−4 and y=[x] and find the points of intersection.
The graphs of the functions are shown in the following figure.
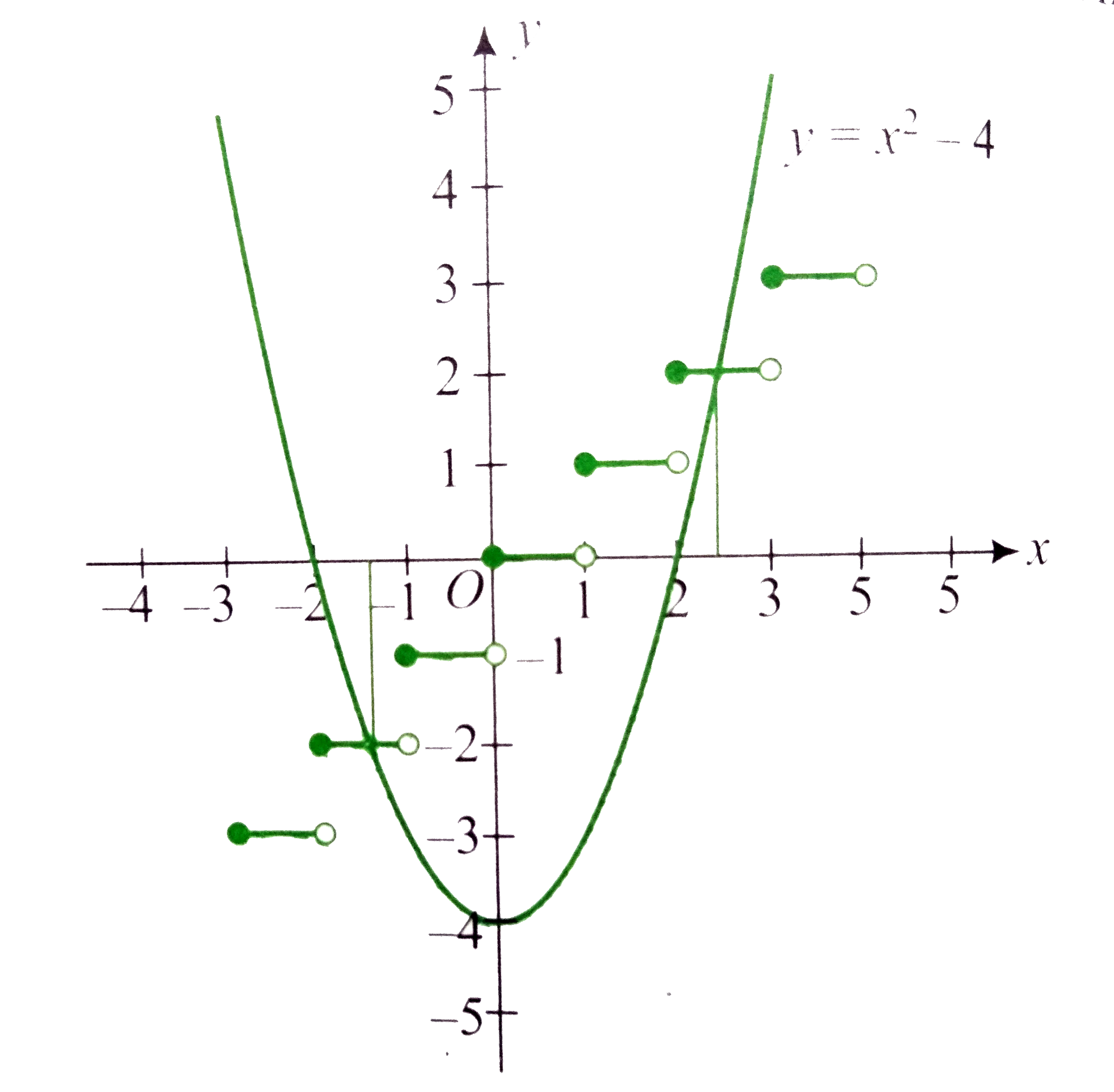
We observe the graphs intersect when x2−4=2 and x2−4=−2
⇒x2=6 or x2=2
⇒x=√6 or −√2
Topper's Solved these Questions
Similar Questions
Let ABCandABC' be two non-congruent triangles with sides AB=4,AC=AC′=2√2 and angle B=300 . The absolute value of the difference between the areas of these triangles is
05:20View SolutionNumber of integral value(s) of λ for which vectors x2ˆi−ˆj+xˆk,(λ−1)ˆi−2λˆj−ˆk and ˆi−ˆj+ˆk, in the order form right-handed system ∀x ∈R, is
(a) 0 (b) 2 (c) 4 (d) 604:32View SolutionSolve x2−4−[x]=0 (where [] denotes the greatest integer function).
04:30View SolutionIf [log_(2)((x)/([x]))]>=0, where [.] denote the greatest integer function,then
03:48View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
04:42View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
02:28View SolutionSolve x^2-4x-[x]=0 (where [] denotes the greatest integer function).
03:30View SolutionSolve : 4{x}=x+[x](where [⋅] denotes the greatest integer function and {⋅} denotes the fractional part function.
02:02View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
01:51View SolutionSolve
limx→0+[sinxx]
(where [.] denotes greatest integer function.)01:28View SolutionSolve
limx→0−[sinxx]
(where [.] denotes greatest integer function.)01:41View SolutionSolve
limx→0+[tanxx]
(where [.] denotes greatest integer function.)04:48View SolutionSolve
limx→0−[tanxx]
(where [.] denotes greatest integer function.)02:00View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
05:13View SolutionSolve : 4{x}= x+ [x] (where [*] denotes the greatest integer function and {*} denotes the fractional part function.
06:11View SolutionSolve x^2-4-[x]=0 (where [] denotes the greatest integer function).
03:39View Solution

