Solve $∣ ∣ x^{2} + 4 x + 3 ∣ ∣ + 2 x + 5 = 0 .$

Video Solution

Text Solution

Verified by Experts

We have $∣ ∣ x^{2} + 4 x + 3 ∣ ∣ + 2 x + 5 = 0$
or $∣ ∣ x^{2} + 4 x + 3 ∣ ∣ = - (2 x + 5)$
Roots of equation are values of x where the graphs of $y = ∣ ∣ x^{2} + 4 x + 3 ∣ ∣ and y = - (2 x + 5)$

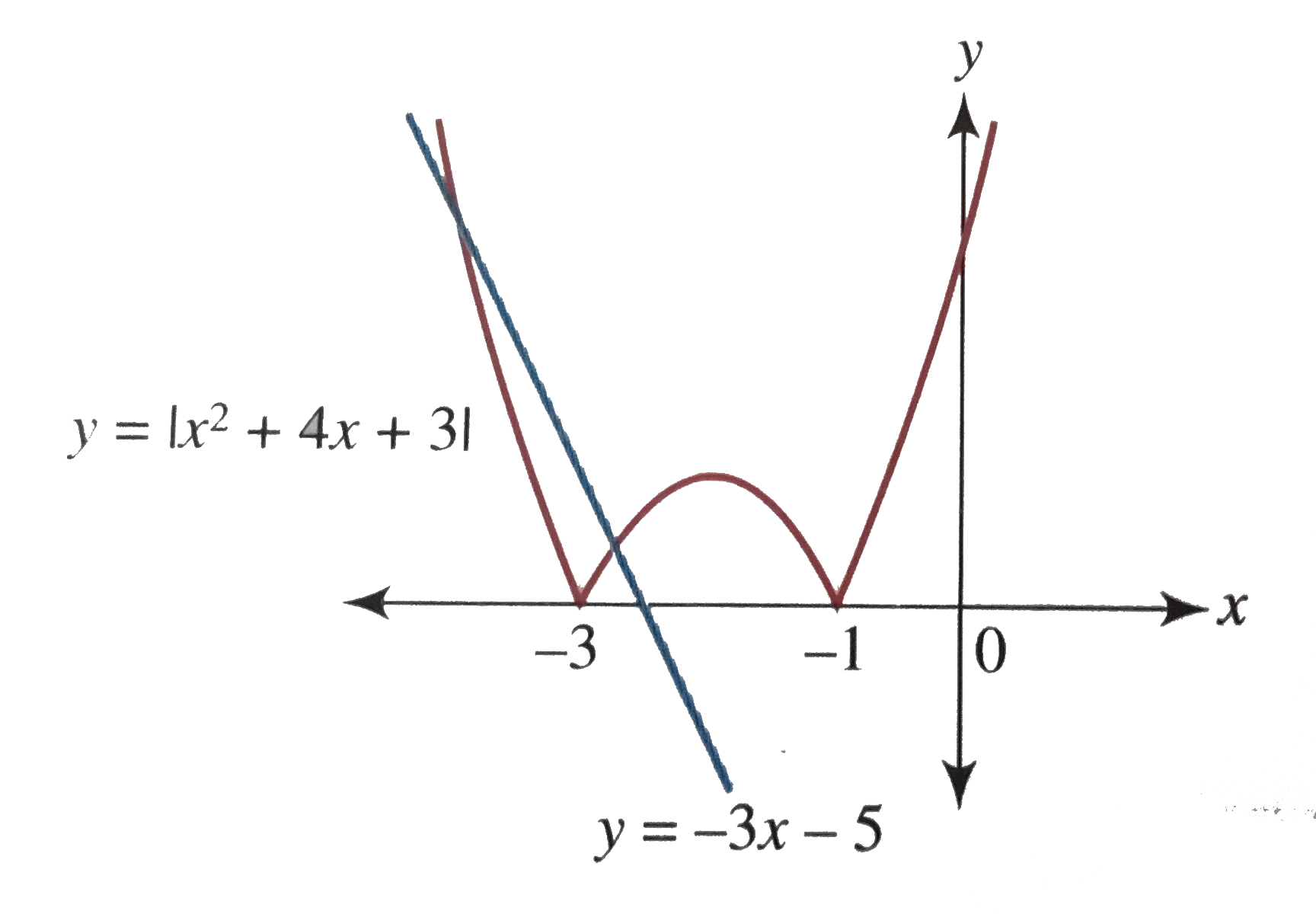
From the graph, one root $x < - 3$ and one root for $- 3 < x < - 1$ .
For $x < - 3$ ,
$x^{2} + 4 x + 3 = - 2 x - 5$
or $x^{2} + 6 x + 8 = 0$
$\Rightarrow (x + 4) (x + 2) = 0$
$\Rightarrow x = - 4 (a s x < - 3)$
For $- 3 < x < - 1$ ,
$- (x^{2} + 4 x + 3) = - (2 x + 5)$
$\Rightarrow x^{2} + 2 x - 2 = 0$
$\Rightarrow x = (- 2 \pm \sqrt{4 + 8} = - 1 \sqrt{3} (a s - 3 < x < - 1)$
Hence $x = - 4, - 1 - \sqrt{3}$

Updated on:21/07/2023

|

Class 12 MATHS LINEAR PROGRAMMING

Topper's Solved these Questions

Similar Questions

CENGAGE-GRAPHICAL TRANSFORMATIONS-Exercise

Home
Ask Doubt
Profile