state whether the statement are true (T) or false (F)
Let ab be a two-digit number, then ab + ba is divisible by 9.
To determine whether the statement "Let ab be a two-digit number, then ab + ba is divisible by 9" is true or false, we can follow these steps:
1. Understanding the Two-Digit Number:
- Let the two-digit number be represented as ab, where a is the tens digit and b is the units digit.
- In numerical terms, ab can be expressed as 10a+b.
2. Understanding the Reverse Number:
- The reverse of the number ab is ba, which can be expressed as 10b+a.
3. Adding the Two Numbers:
- Now, we need to find ab+ba:
ab+ba=(10a+b)+(10b+a)
- Simplifying this, we get:
ab+ba=10a+b+10b+a=11a+11b
4. Factoring Out the Common Term:
- We can factor out 11 from the expression:
ab+ba=11(a+b)
5. Checking for Divisibility by 9:
- The expression 11(a+b) indicates that the sum ab+ba is divisible by 11, but we need to check if it is divisible by 9.
- For ab+ba to be divisible by 9, a+b must be such that 11(a+b) is divisible by 9.
6. Conclusion:
- Since 11 is not divisible by 9, 11(a+b) can only be divisible by 9 if a+b itself is a multiple of 9.
- However, a+b can take values from 0 to 18 (as a and b are digits), and not all combinations will yield a sum that is a multiple of 9.
- Therefore, the statement is False.
Final Answer:
The statement "Let ab be a two-digit number, then ab + ba is divisible by 9" is False (F).
- Let the two-digit number be represented as ab, where a is the tens digit and b is the units digit.
- In numerical terms, ab can be expressed as 10a+b.
- The reverse of the number ab is ba, which can be expressed as 10b+a.
- Now, we need to find ab+ba:
ab+ba=(10a+b)+(10b+a)
- Simplifying this, we get:
ab+ba=10a+b+10b+a=11a+11b
- We can factor out 11 from the expression:
ab+ba=11(a+b)
- The expression 11(a+b) indicates that the sum ab+ba is divisible by 11, but we need to check if it is divisible by 9.
- For ab+ba to be divisible by 9, a+b must be such that 11(a+b) is divisible by 9.
- Since 11 is not divisible by 9, 11(a+b) can only be divisible by 9 if a+b itself is a multiple of 9.
- However, a+b can take values from 0 to 18 (as a and b are digits), and not all combinations will yield a sum that is a multiple of 9.
- Therefore, the statement is False.
The statement "Let ab be a two-digit number, then ab + ba is divisible by 9" is False (F).
Topper's Solved these Questions
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Exercise (Write the correct answer)
17 Videos
- PLAYING WITH NUMBERS BOOK - NCERT EXEMPLARCHAPTER - PLAYING WITH NUMBERS EXERCISE - Exercise (Fill in the blanks)
16 Videos
- MENSURATIONBOOK - NCERT EXEMPLARCHAPTER - MENSURATIONEXERCISE - THINK AND DISCUSS
2 Videos
- RATIONAL NUMBERS BOOK - NCERT EXEMPLARCHAPTER - RATIONAL NUMBERS EXERCISE - Think and Discuss
1 Videos
Similar Questions
State whether the statements are true or falsea−b=b−a
View Solutionstate whether the statement are true (T) or false (F).
 is a concave polygon.
is a concave polygon.
View SolutionState whether the statements are true or falsea×b=b×a
View Solutionstate whether the statement are true (T) or false (F).
 is a simple closed curve.
is a simple closed curve.
View SolutionState whether the statements are true or falsea÷(−b)=−(a÷b)
View Solutionstate whether the statement are true (T) or false (F).
Every kite is a trapezium.
View SolutionState whether the statements are true (T) or false (F).
1L = 1000 cm3
View SolutionState whether the statement given is true (T) or false (F):
A two-digit number ab is always divisible by 2 if b is an even number.
View Solutionstate whether the statement are true (T) or false (F)
A three-digit number 42x is divisible by 9. Find the value of x.
View SolutionState whether the statements are true (T) or (F) false.
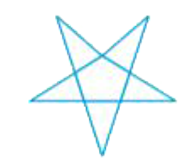 is a polygon.
is a polygon.
View Solution
