Statement I The graph of is symmetrical about the Y-axis.
Statement II The graph of is symmetrical about the origin.
Both Statement I and Statement II are correct and Statement II is the correct explanation of Statement I
Both Statement I and Statement II are correct but Statement II is not the correct explanation of Statement I
Statement I is correct but Statement II is incorrect
Statement II is correct but Statement I is incorrect
The correct Answer is:A
Step by step video & image solution for Statement I The graph of y=sec^(2)x is symmetrical about the Y-axis. Statement II The graph of y=tax is symmetrical about the origin. by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Topper's Solved these Questions
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Passage Based Questions)4videos
GRAPHICAL TRANSFORMATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (Subjective Type Questions)3videos
GRAPHICAL TRANSFORMATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise (More Than One Correct Option Type Questions)3videos
GRAPHICAL TRANSFORMATIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - FUNCTIONSEXERCISE - FUNCTION EXERCISE 8:Questions Asked in Previous 10 Years Exams1videos
FUNCTIONS
- BOOK - ARIHANT MATHS ENGLISHCHAPTER - HYPERBOLAEXERCISE - Hyperbola Exercise 11 : Questions Asked in Previous 13 Years Exams3videos
HYPERBOLA
Similar Questions
Knowledge Check
- Question 1 - Select One
Which of the following graphs is symmetric about the origin ?
A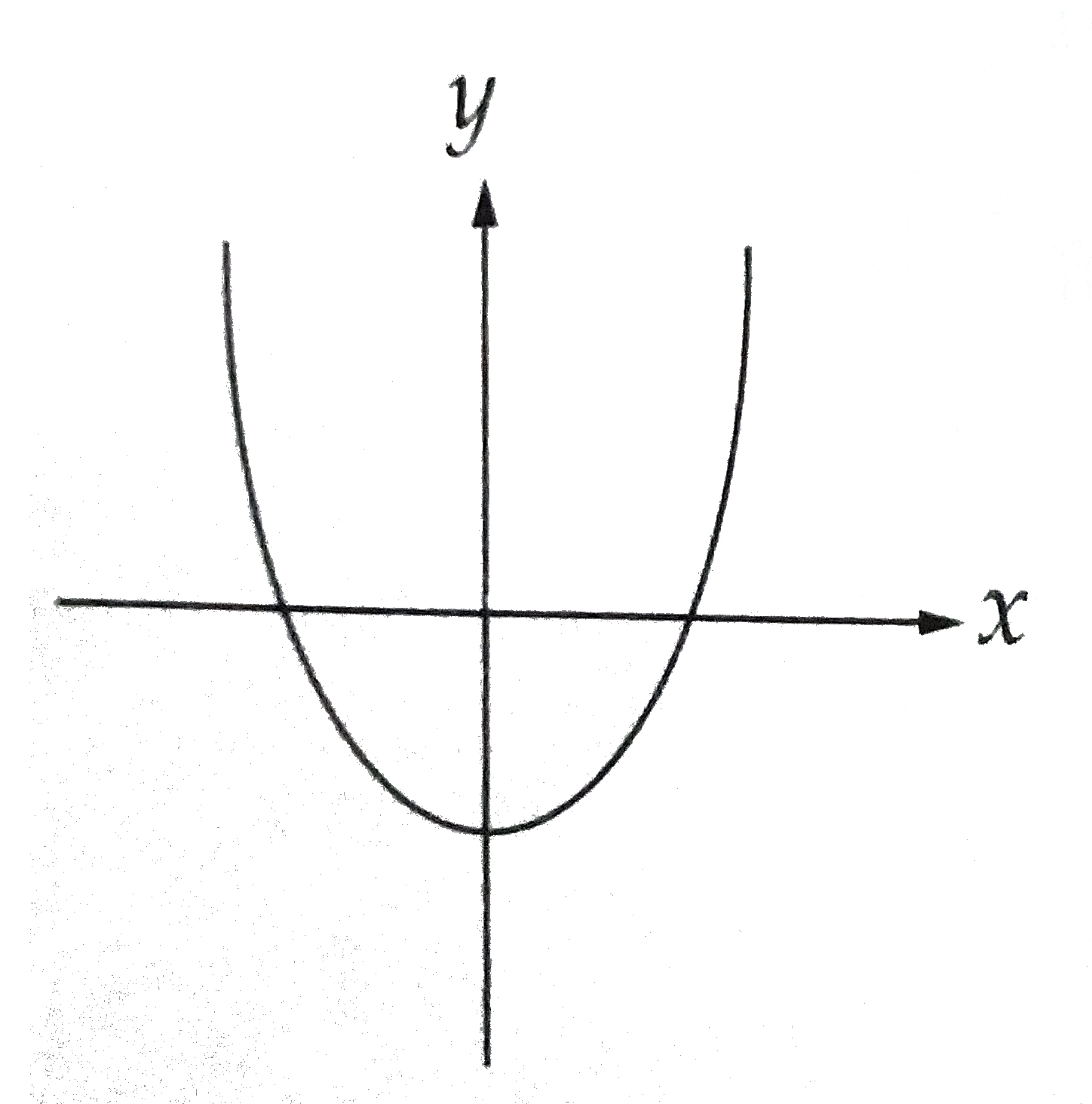
B
C
D
If the graph of a function f(x) is symmetrical about the line x = a, then
View SolutionWhich of the following is a function whose graph is symmetrical about the origin ?
View SolutionIf graph of y=f(x) is symmetrical about the y-axis and that of y=g(x) is symmetrical about the origin and if h(x)=f(x).g(x),thend3h(x)dx3atx=0 is (a)cannot be determined (b) f(0).g(0) (c)0 (d) none of these
View SolutionIf graph of y=f(x) is symmetrical about the y-axis and that of y=g(x) is symmetrical about the origin and if h(x)=f(x).g(x),thend3h(x)dx3atx=0 is cannot be determined (b) f(0).g(0) 0 (d) none of these
View SolutionIf the graph of the function y = f(x) is symmetrical about the line x = 2, then
View SolutionStatement I The curve y=x22+x+1 is symmetric with respect to the line x=1. because Statement II A parabola is symmetric about its axis.
View SolutionStatement 1: The function f (x) = sin x is symmetric about the line x = 0.
Statement 2: Every even function is symmetric about y-axis.View Solution