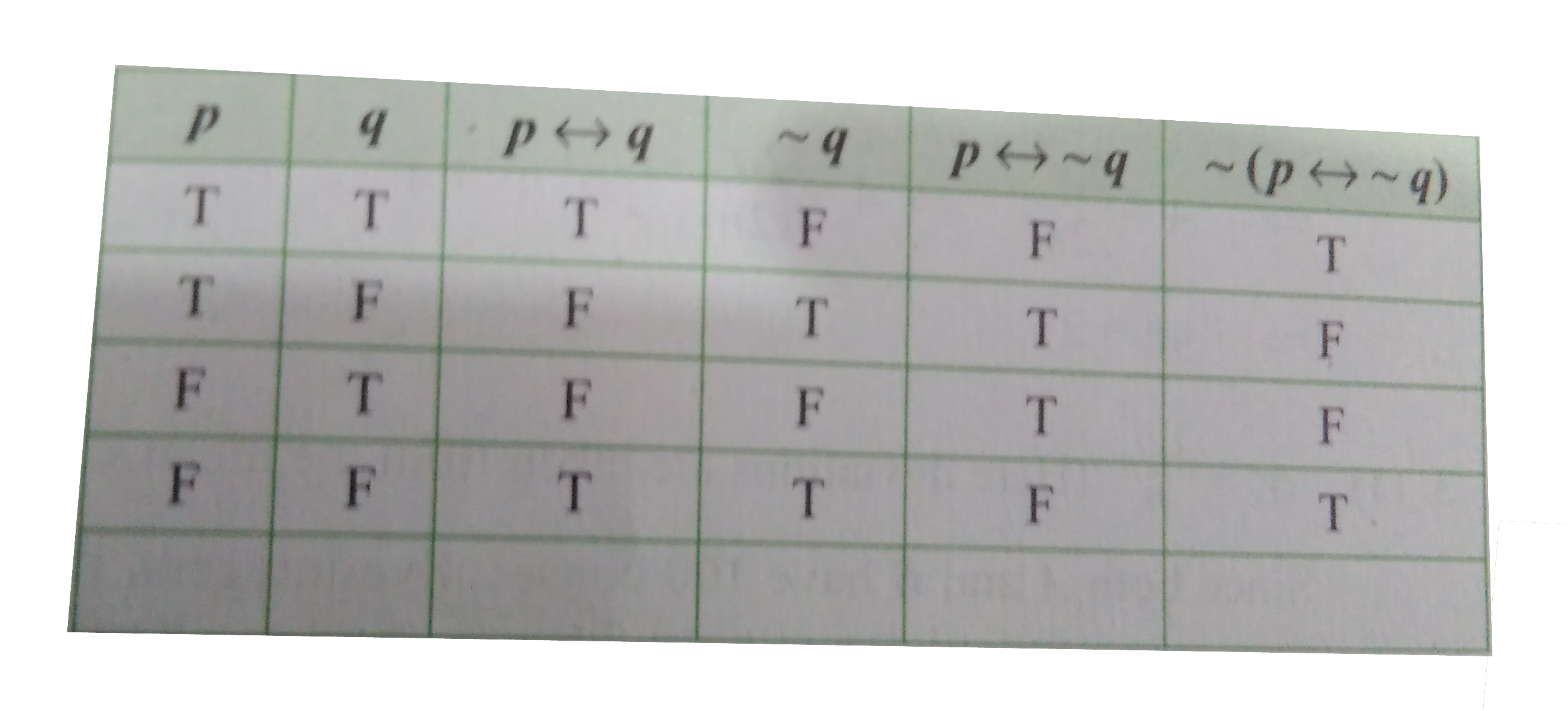Statements -1 : ~(p↔~q) is equivalent to p↔q
Statement-2: (~p↔~q) is a tautology.
A
Statement-1 is true, statement 2 is true, statement 2 is a correct explanation for statement 1
B
Statement 1 is true, statement-2 is true, statement 2 is not a correct explanation for statement 1
C
Statement 1 is true , statement 2 is false,
D
statement 1 is false, statement 2 is true
Video Solution
Text Solution
The correct Answer is:C
|
Topper's Solved these Questions
- MATHMETICAL REASONINGBOOK - CENGAGECHAPTER - MATHMETICAL REASONINGEXERCISE - Exercise (Single)
38 Videos
- LOGARITHM AND ITS PROPERTIESBOOK - CENGAGECHAPTER - LOGARITHM AND ITS PROPERTIESEXERCISE - JEE Previous Year
5 Videos
- MATRICESBOOK - CENGAGECHAPTER - MATRICESEXERCISE - Solved Examples And Exercises
165 Videos
Similar Questions
Knowledge Check
~(p↔q) is equivalent to
A~(p↔q)∨(q∧~p)B(p∨~q)∧(q∨~q)C(p→q)∧(q→p)D(q→p)∨(p→q)Statement-1 : ~(p⇔~q) is equivalent to p⇔q.
Statement-2: ~(p⇔q) is a tautologyAStatement-1 is true, statement-2 is true, statement-2 is correct explanation for statement-1BStatement-1 is true, statement-2 is true, statement-2 is not a correct explanation for statement-1CStatement-1 is true, statement-2 is falseDStatement-1 is false. statement-2 is trueStatement-1 : ~(p⇔~q) is equivalent to p⇔q.
Statement-2: ~(p⇔q) is a tautologyAStatemetn-1 is true, Statement-2 is true, Statemetn-2 is not a correct explanation for Statement-1BStatement-1 is treu, Statement-2 is falseCStatement-1 is false Statement-2 is trueDStatemene-1 is true, Statement-2 is true Statemetn-2 is a correct explanation for Statement-1