Supose that 80 % of all families own a elevision set. If 10 families are interviewed at random, find the probability that seven famileis own a television set .
Let x be the no. of families who own a television set.
P (families who own a television set) =P=80%=80100=0.8.
q=1−p=1−0.8=0.2
Given : n=10
X:~B(n,p)∴X~B(10,0.8)
The p.m.f of X is given by
P(X=x)=nCx.Px.qn−x,x=1,2,.........n,
∴P(X=x)=10Cx.(0.8)x.(0.2)10−x,x=1,2,.........10,
P (at most 3 families own a television set)
⇒P(x≤3)=P(x=0)+P(x=1)+P(x=2)+P(x=3)
=10C0.(0.8)0(0.2)10+10C1(0.8)1(0.2)9+10C2(0.8)0(0.2)10+10C2(0.8)2(0.2)8+10C3(0.8)3(0.2)7
=1×1×10241010+10×0.8×512109+45×0.64×256108+120×(0.512)×128107
=1024+40960+737280+78643201010=86435841010=0.00086
Topper's Solved these Questions
- JULY 2018BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2018EXERCISE - SECTION II
20 Videos
- JULY 2017BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - JULY 2017EXERCISE - SECTION - II
20 Videos
- MARCH 2014BOOK - GURUKUL PUBLICATION - MAHARASHTRA PREVIOUS YEAR PAPERSCHAPTER - MARCH 2014EXERCISE - SECTION-II
20 Videos
Similar Questions
Suppose that 80% of all families own a television set. If 5 families are inervised at random, find the probability that :
(a) three families own a television set.
(b) at least two families own a television set.
View SolutionA company selected 2300 families at random and surveyed them to determine a relationship between income level and the number of vehicles in a home The information gathered is listed in the table below : if a family is chosen at random, find the probability that the family is: (i) earning Rs.7000-13000 per month and owning exactly 1 vehicle (ii) owning not more than one vehicles. more than 2 vehicles (lii) earning more than Rs. 13000 and owning 2 or (iv) owning no vehicle
View Solution
Knowledge Check
80% of all families own a television set. If 10 families are interviewed at random, then the probability that at most three families own a television set is
A(8401)(0.8)10B(8401)(0.2)10C(8441)(0.8)10D(8441)(0.2)10In a locality 100 families were chosen at random and the following data was collected:
∣∣ ∣ ∣∣Number of childeren 0 1 2 3 4 or moreis each familyNumber of families 3 40 45 12 0∣∣ ∣ ∣∣
If a family is chosen at random, find the probability that the chosen family has 3 or more children.A2225B325C425D15The set S’ = {n : n is an integer, 1≤n≤50}. If an element of S is selected at random, find the probability that it does not contain the digit '2' at all.
A725B1825C1750D710
The following data about number of girls in a family was recorded.

A family is chosen at random. Find the probability of having 2 girls in the chosen family.
View SolutionAn organisation selected 2400 families at random and surveyed them to determine a relationship between the income level and the number of vehicles in a family . The information gathered is listed in the table below :
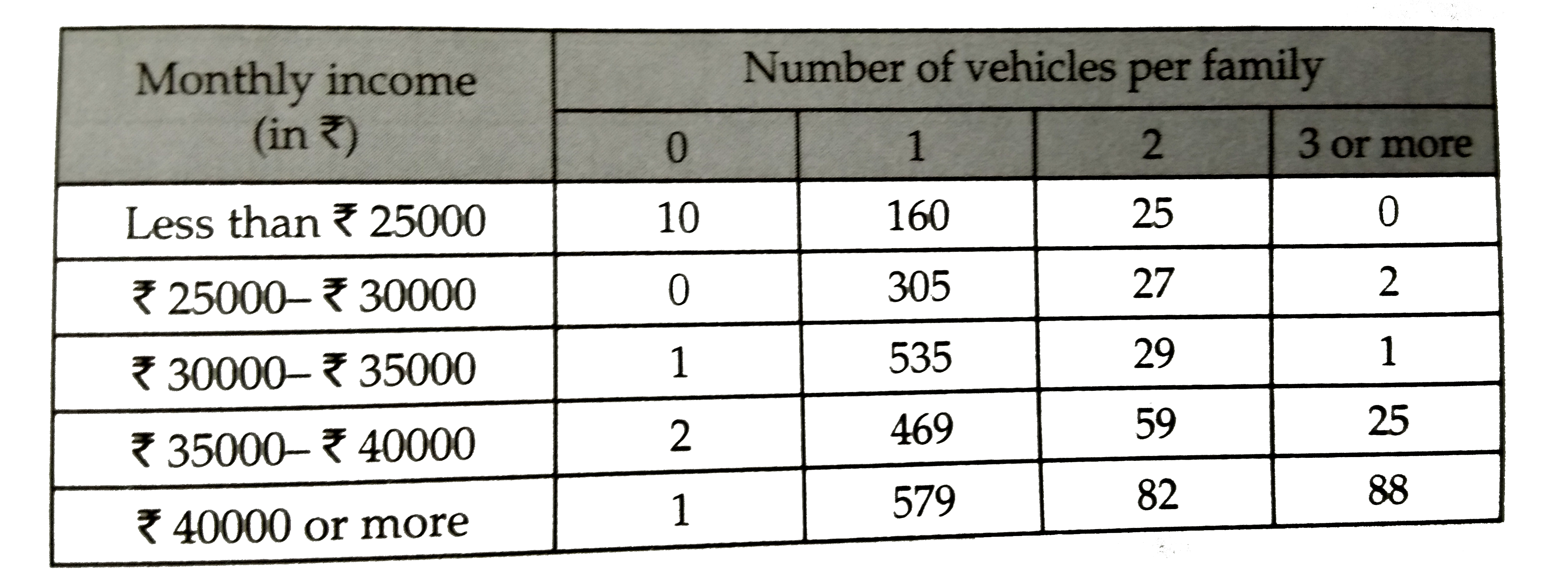
Suppose a family is chosen at random . Find the probability that the family chosen is
(i) earning ₹ 25000 - ₹ 30000 per month and owning exactly 2 vehicles .
(ii) earning ₹ 40000 or more per month and owing exactly 1 vehicle.
(iii) earning less than ₹ 25000 per month and not owing any vehicle .
(iv) earning ₹ 35000 - ₹ 40000 per month and owning 2 or more vehicles.
(v) Owing not more than 1 vehicle .
View Solution1000 families with 2 children were selected randomly and the following data were recorded.
∣∣∣Number of boys in a family 0 1 2Number of families 140 560 300∣∣∣
If a family is chosen at random, find the probability that it has (i) no boy (ii) one boy (iii) two boys (iv) at least one boy (v) at most one boy.
View SolutionIn a certain town, 60% of the families own a car, 30% own a house and 20% own both car and house. If a family is randomly chosen, then what is the probability that this family owns a car or a house but not both?
View SolutionIn a large metropolitan area, the probabilities are 0.87,0.36,0.30 that a family (randomly chosen for a sample survey) owns a colour televise set, a black and white television set, or both kinds of sets. What is the probability that a family owns either any one or both kinds of sets?
View Solution
