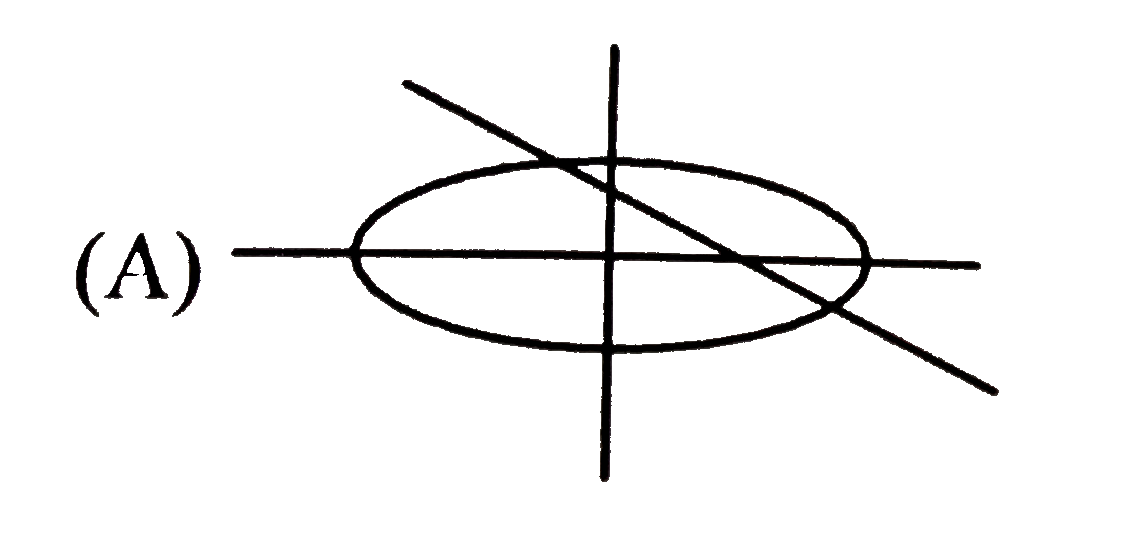
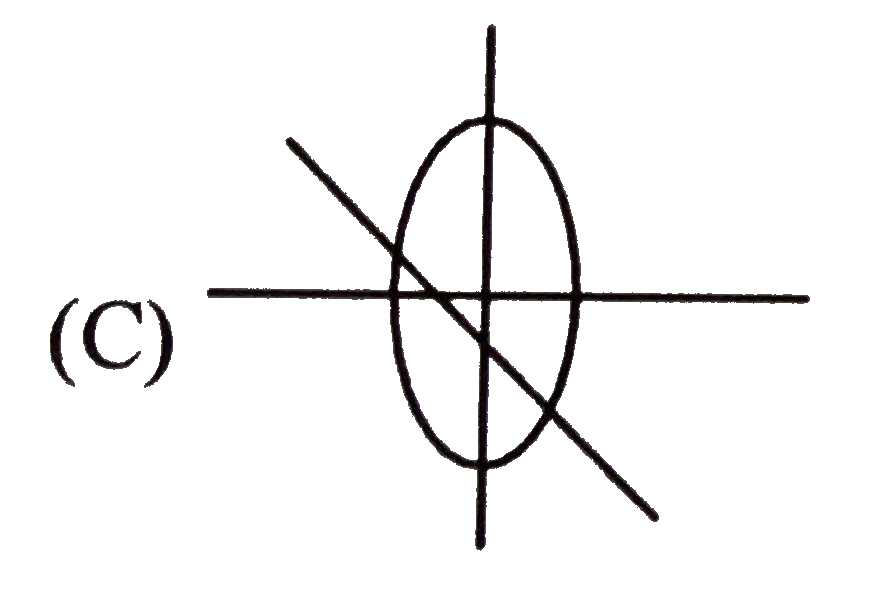
Suppose a, b are real numbers such that ab≠0. Which of the following four figures represents the curve (y−ax−b)(bx2+ay2−ab)=0 ?
A
B

C
D
Video Solution
Text Solution
The correct Answer is:B
y=ax+b and x2a+y2b=1
slope =a
for the line, y intercept =b
Fig 1. for line →a<0,b>0 hence the other fig. Cannot be an ellipse
Fig.2 a>0,b<0 hence the fig. is a hyperbola
Similarly you can check rest 2 options
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
Let a, b and c be real numbers such that 4a+2b+c=0 and ab>0. Then the equation ax^(2) + bx + c = 0 has
Acomplex rootsBexactly one rootCreal rootsDnone of theseLet a, b and c bereal numbers such that 4a+2b+c=0 and ab > 0. Then the quadratic equation ax2+bx+c=0 has
Areal rootsBcomplex rootsCpurely imaginary rootsDonly one rootIf a,b,c ∈R, then for which of the following graphs of the quadratic polynomial y=ax2−2bx+c(a≠0), the product (abc) is negative ?
A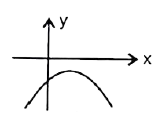 B
B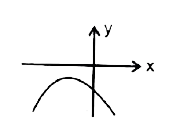 C
C D
D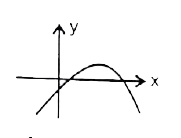
If a,b,c are real numbers and Δ>0 then the roots of ax2+bx+c=0are
View SolutionLet a,bandc be three real numbers, such that a+2b+4c0. Then the equation ax2+bx+c=0
View SolutionIf a,b,c, are real number such that ac≠0, then show that at least one of the equations ax2+bx+c=0 and −ax2+bx+c=0 has real roots.
View SolutionFactorize each of the following expressions:
(i)a2−b+aba (ii) xy−ab+bx−ay
View SolutionIf a, b, c are real numbers in A.P., then the roots of ax2+bx+c=0 are real for
View Solution
