Suppose ABCS (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0Solution in Bengali
secB=secB
cotA+cotC=0
cosecA=cosecC
tanB+tanD=0
The correct Answer is:B, C, D
Opposite angles of a cyclic quadrilateral are supplementary.
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Linked Comprehension Type
11 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Matrix Match Type
3 Videos
- TRIGONOMETRIC FUNCTIONS BOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC FUNCTIONS EXERCISE - Exercises
57 Videos
- TRIGONOMETRIC EQUATIONSBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC EQUATIONSEXERCISE - Archives (Numerical value type)
4 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBOOK - CENGAGE PUBLICATIONCHAPTER - TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASEXERCISE - Archives (Numerical Value Type)
2 Videos
Similar Questions
Let us consider the equation cos^4x/a xa+sin4xb=1a+b,x∈[0,π2],a,b>0 the value of sin8xb3+cos8xa3 is
View Solution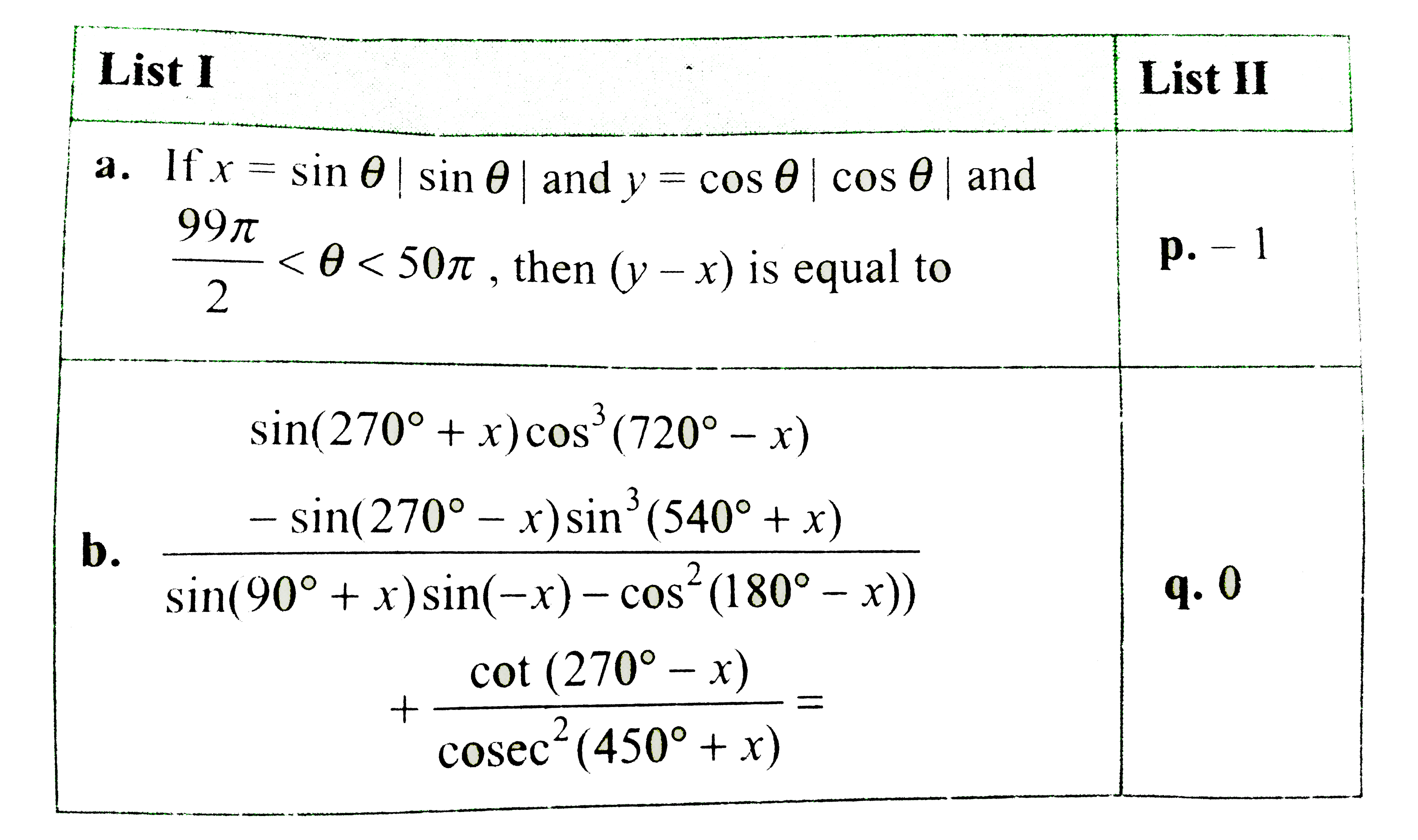
View SolutionIf tanθ=3, then sinθ−cosθsinθ+cosθ is equal to
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionIf A,B,C,D be the angles of a quadrilateral, prove that : tanA+tanB+tanC+tanDcotA+cotB+cotC+cotD=tanAtanBtanCtanD
View SolutionIf A+B+C=π, prove that : (tanA+tanB+tanC)(cotA+cotB+cotC)=1+secAsecBsecC.
View SolutionIf A+B+C=π , prove that cotA+cotB+cotC−cosecA.cosecB.cosecC=cotA.cotB.cotC.
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionSuppose ABCS (in order) is a quadrilateral inscribed in a circle. Which of the following is/are always true? secB=secD (b) cotA+cotC=0 cosecA=cosecC (d) tanB+tanD=0
View SolutionIf A+B+C=π , prove that cotA+cotB+cotC−cosecA.cosecB.cosecC=cotA.cotB.cotC.
View SolutionProve the following identities: 1cosecA−cotA−1sinA=1sinA−1cosecA+cotA
View SolutionProve the following identities: cotA+cosecA−1cotA−cosecA+1=1+cosAsinA
View SolutionSuppose ABCD (in order) is a quadrilateral inscribed in a circle. Which of a following is/are always true ?
View SolutionIf A,B,C,D be the angles of a quadrilateral, prove that : tanA+tanB+tanC+tanDcotA+cotB+cotC+cotD=tanAtanBtanCtanD
View Solution
