Suppose that F(α) denotes the area of the region bounded by x=0,x=2,y2=4x and y=|αx−1|+|αx−2|+αx, where α∈{0,1}. Then the value of F(α)+8√23 when α=0 is (A) 4 (B) 5 (C) 6 (D) 9
5
6
7
9
The correct Answer is:a
When α=1 F(1) is the area of the shaded region bounded by x=0,x=2,y2=4xandy=|x−1|+|x−2|+x
or, y=⎧⎪⎨⎪⎩−x+3,x<1x+1,1≤x<23x−3,x≥2
as shown in Fig. 31
∴F(1)=1∫0(y2−y1)dx+2∫1(y4−y3)dx
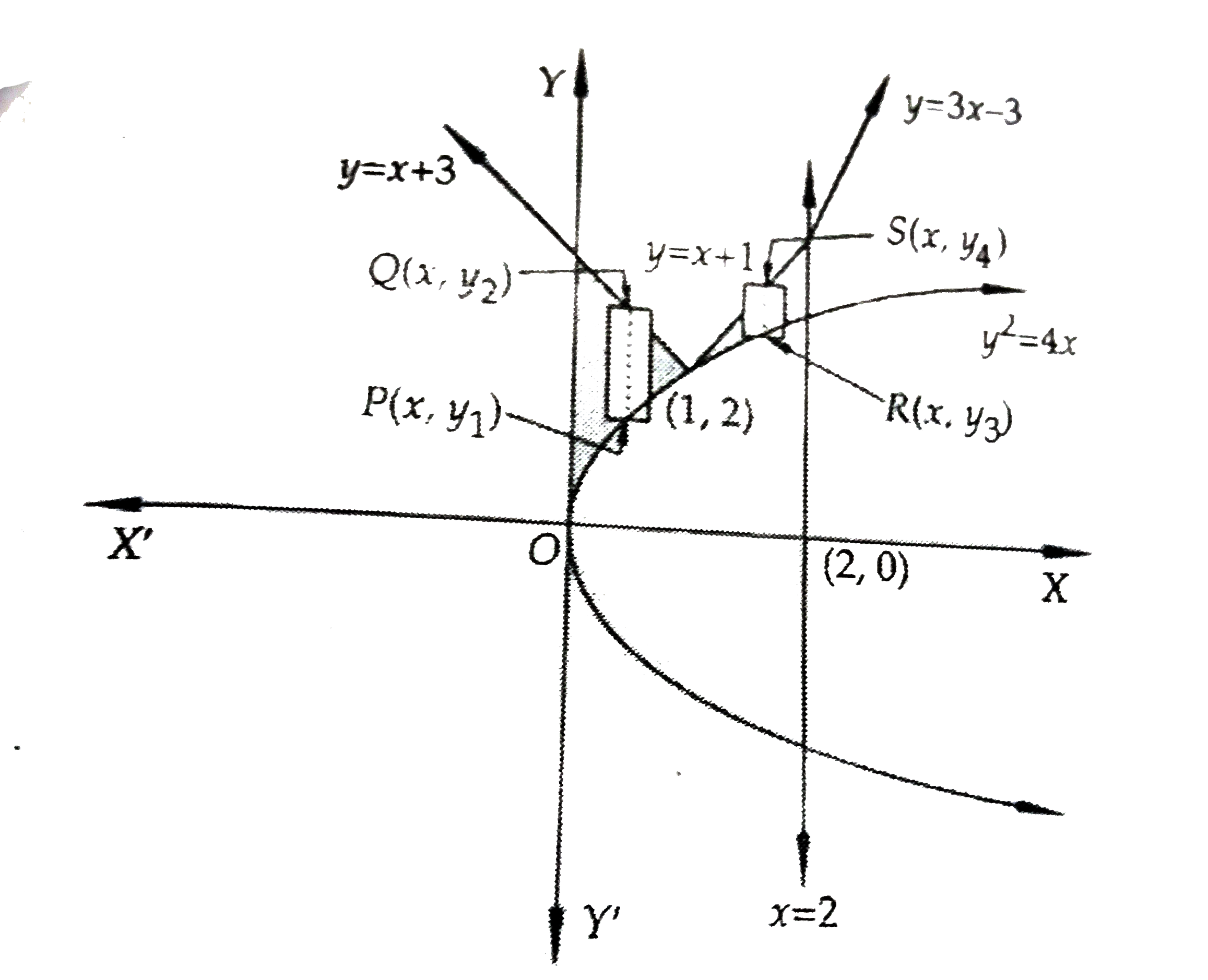
⇒F(1)=1∫0(−x+3−2√x)dx+2∫1(x+1−2√x)dx
⇒F(1)=[−x22+3x−43x3/2]10+[x22+x−43x3/2]21
⇒F(1)=(−123−43)+(2+2−8√23−12−1+43)
F(1)=5−83√2
⇒F(1)+83√2=5
Topper's Solved these Questions
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Exercise
61 Videos
- AREAS OF BOUNDED REGIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - AREAS OF BOUNDED REGIONSEXERCISE - Chapter Test
60 Videos
- ALGEBRAIC INEQUATIONSBOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - ALGEBRAIC INEQUATIONSEXERCISE - Exercise
39 Videos
- CARTESIAN PRODUCT OF SETS AND RELATIONS BOOK - OBJECTIVE RD SHARMA ENGLISHCHAPTER - CARTESIAN PRODUCT OF SETS AND RELATIONS EXERCISE - Chapter Test
30 Videos
Similar Questions
Let f(x)=αxx+1 Then the value of α for which f(f(x)=x is
View SolutionIf x=2α+1 and y=α−1 is a solution of the equation 2x−3y+5=0 , find the value of α
View SolutionIf two curves y=2sin(5πx6) and y=αx2−3αx+2α+1 touch each other at some point then the value of √3α5π is (0≤x≤185)
View SolutionIf x+4y=14 is a normal to the curve y2=αx3−β at (2,3), then the value of α+β is
View SolutionIf f(x) is a non - negative function such that the area bounded by y=f(x), x - axis and the lines x = 0 and x=α is 4αsinα+2 sq. Units
(∀α∈[0,π]), then the value of f(π2) is equal to
View SolutionThe value of ∫π20sin|2x−α|dx, where α∈[0,π], is (a) 1−cosα (b) 1+cosα (c) 1 (d) cosα
View SolutionIf α,β are the roots of the equation x2+αx+β=0 such that α≠β and ||x−β|−α|∣<α, then
View SolutionFind the value of α so that limx→01x2(eαx−ex−x)=32
View SolutionLet f(x)=αxx+1,x≠−1. Then write the value of α satisfying f(f(x))=x for all x≠−1.
View SolutionLet f(x)=αx(x+1),x≠−1. for what value of α is f(f(x))=x? (a)√2 (b) −√2 (c) 1 (d) −1
View Solution
