Suppose that six students, including Madhu and Puja, are having six beds arranged in a row. Further, suppose that Mudhu does not want a bed adjacent to Puja. Then the number of ways, the beds can be allotted to students is
The correct Answer is:C
To solve the problem of how many ways six students can be allotted beds such that Madhu and Puja are not adjacent, we can follow these steps:
Step 1: Calculate the total arrangements without restrictions
First, we calculate the total number of arrangements of the six students without any restrictions. The number of arrangements of 6 students is given by the factorial of 6:
6!=720
Step 2: Calculate the arrangements where Madhu and Puja are together
Next, we consider the scenario where Madhu and Puja are treated as a single unit or block since they do not want to be adjacent. If we treat Madhu and Puja as one block, we effectively have 5 units to arrange: the Madhu-Puja block and the other 4 students.
The number of ways to arrange these 5 units is given by:
5!=120
Step 3: Account for the arrangements within the block
Within the Madhu-Puja block, Madhu and Puja can be arranged in 2 ways (Madhu can be on the left or Puja can be on the left). Thus, we multiply the arrangements of the blocks by the arrangements within the block:
5!×2!=120×2=240
Step 4: Subtract the restricted arrangements from the total arrangements
Now, we subtract the number of arrangements where Madhu and Puja are together from the total arrangements to find the arrangements where they are not adjacent:
6!−(5!×2!)=720−240=480
Final Answer
Thus, the number of ways the beds can be allotted to the students such that Madhu and Puja are not adjacent is:
480
First, we calculate the total number of arrangements of the six students without any restrictions. The number of arrangements of 6 students is given by the factorial of 6:
Next, we consider the scenario where Madhu and Puja are treated as a single unit or block since they do not want to be adjacent. If we treat Madhu and Puja as one block, we effectively have 5 units to arrange: the Madhu-Puja block and the other 4 students.
Within the Madhu-Puja block, Madhu and Puja can be arranged in 2 ways (Madhu can be on the left or Puja can be on the left). Thus, we multiply the arrangements of the blocks by the arrangements within the block:
Now, we subtract the number of arrangements where Madhu and Puja are together from the total arrangements to find the arrangements where they are not adjacent:
Thus, the number of ways the beds can be allotted to the students such that Madhu and Puja are not adjacent is:
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section I - Solved Mcqs
111 Videos
- PERMUTATIONS AND COMBINATIONSBOOK - OBJECTIVE RD SHARMACHAPTER - PERMUTATIONS AND COMBINATIONSEXERCISE - Section II - Assertion Reason Type
9 Videos
- PARABOLABOOK - OBJECTIVE RD SHARMACHAPTER - PARABOLAEXERCISE - Chapter Test
30 Videos
- PROBABILITY BOOK - OBJECTIVE RD SHARMACHAPTER - PROBABILITY EXERCISE - Chapter Test
45 Videos
Similar Questions
Six X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:
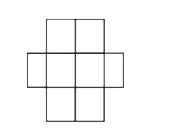
View SolutionSix X have to be placed in the squares of figure such that each row contains at least one X. The number of ways in which this can be done is:

View Solution
Knowledge Check
Suppose that six students, including Madhu and Puja, are having six beds arranged in a row. Further, suppose that Madhu does not want a bed adjacent to Puja. Then the number of ways, the beds can be attotted to studets is :
A264B480C600D384Six X have to be placed in the squares of Fig. 6.6 such that each row contain at least one X. The number of ways in which this can be done is
 A25B26C27D30
A25B26C27D30A group of 2n students consisting of n boys and n girls are to arranged in a row such that adjacent members are of opposite sex. The number of ways in which this can be done is :
A2(n!)B(n!)2C2(n!)2Dn!
Six people are going to sit in a row on a bench. A and B are adjacent, C does not want to sit adjacent to D. E and F can sit anywhere. Number of ways in which these six people can be seated is
View SolutionThe 10 students of Batch B feel they have some conceptual doubt on Circular-permutation. Mr. Mathew called them in discussion room and asked them to sit down around a circular table which is surrounded by 13 chairs. Mr Mathew told that his (Mr. Mathew) adjacent seat should not remain the number of ways, in which the students can sit around a round table ifMr. Mathew also sit on a chair .
View SolutionSix teachers and six students have to sit round a circular table such that thereis a teacher between any two students. The number of ways in which they can sit is
View SolutionA team of 8 students goes on an excursion, in two cars, of which one can seat 5 and the other only 4. If internal arrangement inside a car does not matter then the number of ways they can travel is
View SolutionIn an examination hall there are four rows of chairs. Each row has 8 chairs one behind the other. There are two classes sitting for the examination with 16 students in each class. It is desired that i each row, all students belong to the same class and that no two adjacent row are allotted to the same class. In how many ways can these 32 students be seated?
View Solution
