Suppose the sides of a triangle form a geometric progression with common ratio r. Then r lies in the interval-

A

$(0, \frac{- 1 + \sqrt{5}}{2})$

B

$(\frac{1 + \sqrt{5}}{2}, \frac{2 + \sqrt{5}}{2})$

C

$(\frac{- 1 + \sqrt{5}}{2}, \frac{1 + \sqrt{5}}{2})$

D

$(\frac{2 + \sqrt{5}}{2}, \infty)$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:C

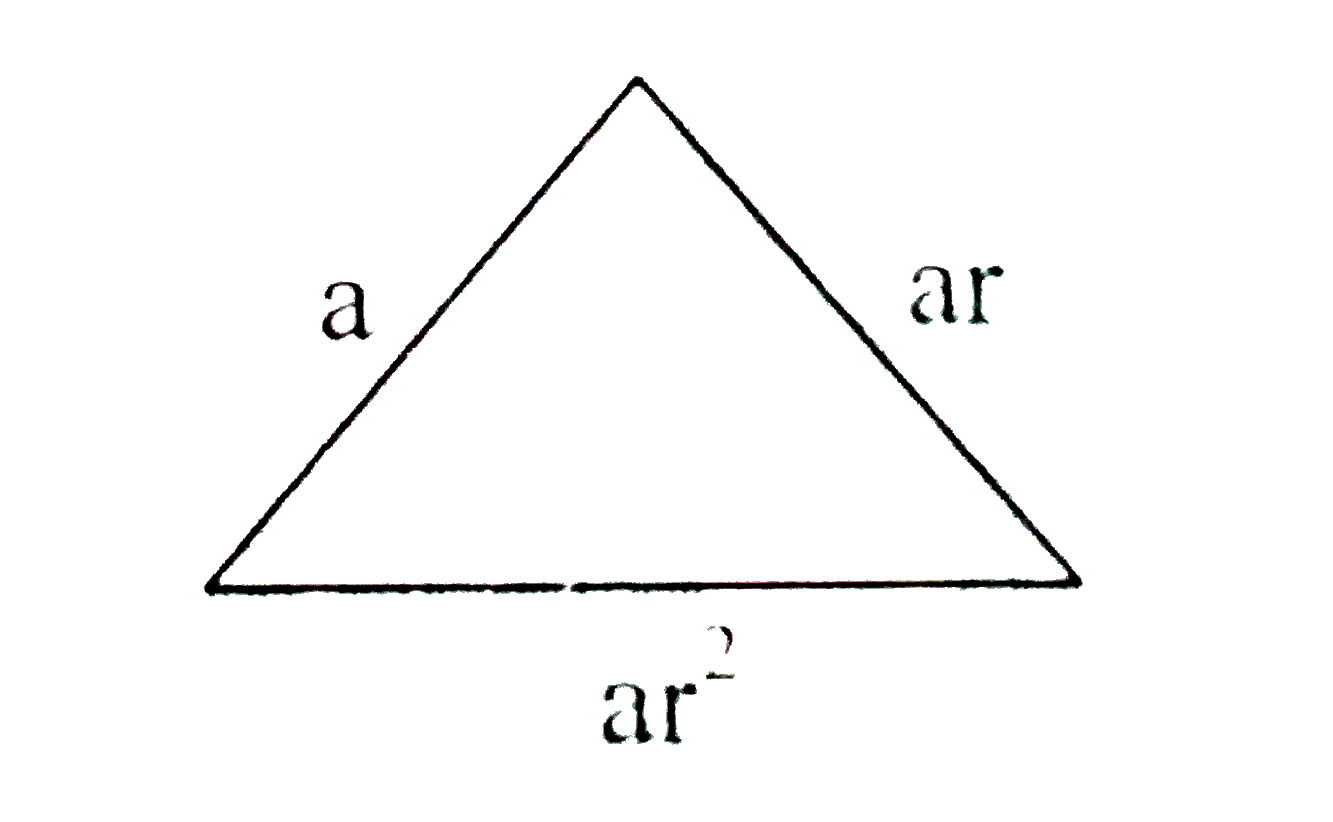
$a + a r > a r^{2}$
$r^{2} - r - 1 < 0$
$r \in (\frac{1 - \sqrt{5}}{2}, \frac{1 + \sqrt{5}}{2}) \dots\dots.. (1)$
$a r^{2} + a r > 0$
$r > \frac{- 1 + \sqrt{5}}{2}, r < \frac{- 1 - \sqrt{5}}{2} \dots.. (2)$
$a r^{2} + a > a r, r^{2} - 1 + 1 > 0$ always true
Solving (1) & (2)
$r \in (\frac{\sqrt{5} - 1}{2}, \frac{\sqrt{5} + 1}{2})$

Updated on:21/07/2023

|

Class 12 MATHS QUESTION BANK

Topper's Solved these Questions

Similar Questions

Knowledge Check

the sum of the first 8 terms of a geometric progression is 6560 and the common ratio is 3. the first term is
A1
B2
C3
D4

KVPY PREVIOUS YEAR-KVPY-exercise

Home
Ask Doubt
Profile