Suppose x and y are real numbers such that −1<x<y<1 Let G be the sum of the geometric series whose first term is x and whose common ratio is y, and let G' be the sum of the geomateric series whose first term is y and common ratio is x. If G = G' then the value of (x + y) is
1
−1
2
−2
The correct Answer is:A
To solve the problem, we need to find the value of x+y given the conditions and the equality of two geometric series sums G and G′.
1. Define the sums of the geometric series:
- The sum G of the geometric series with first term x and common ratio y is given by:
G=x1−y(for |y|<1)
- The sum G′ of the geometric series with first term y and common ratio x is given by:
G′=y1−x(for |x|<1)
2. Set the sums equal to each other:
G=G′⟹x1−y=y1−x
3. Cross-multiply to eliminate the fractions:
x(1−x)=y(1−y)
Expanding both sides gives:
x−x2=y−y2
4. Rearrange the equation:
x−y=x2−y2
This can be factored using the difference of squares:
x−y=(x−y)(x+y)
5. Factor out x−y:
If x≠y, we can divide both sides by x−y:
1=x+y
If x=y, it contradicts the condition x<y. Thus, we conclude:
x+y=1
6. Final answer:
Therefore, the value of x+y is:
1
- The sum G of the geometric series with first term x and common ratio y is given by:
G=x1−y(for |y|<1)
- The sum G′ of the geometric series with first term y and common ratio x is given by:
G′=y1−x(for |x|<1)
G=G′⟹x1−y=y1−x
x(1−x)=y(1−y)
Expanding both sides gives:
x−x2=y−y2
x−y=x2−y2
This can be factored using the difference of squares:
x−y=(x−y)(x+y)
If x≠y, we can divide both sides by x−y:
1=x+y
If x=y, it contradicts the condition x<y. Thus, we conclude:
x+y=1
Therefore, the value of x+y is:
1
Topper's Solved these Questions
- SEQUENCES AND SERIES BOOK - DISHA PUBLICATIONCHAPTER - SEQUENCES AND SERIES EXERCISE - Exercise -2 : Concept Applicator
30 Videos
- SEQUENCES AND SERIES BOOK - DISHA PUBLICATIONCHAPTER - SEQUENCES AND SERIES EXERCISE - Exercise -2 : Concept Applicator
30 Videos
- RELATIONS AND FUNCTIONS-2BOOK - DISHA PUBLICATIONCHAPTER - RELATIONS AND FUNCTIONS-2EXERCISE - EXERCISE-2: CONCEPT APPLICATOR
30 Videos
- SETSBOOK - DISHA PUBLICATIONCHAPTER - SETSEXERCISE - EXERCISE-2 : CONCEPT APPLICATOR
30 Videos
Similar Questions
Let sk,k=1,2,3,…,100 denote the sum of the infinite geometric series whose first term is k−1⌊k and the common ratio is 1k. Then, the value of
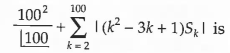 is
is
View SolutionLet G Let G be the sum of infinite geometric series whose first term is sinθ and common ratio is cosθ, while G' be the sum of a different infinite geometric series whose first term cosθ and common ratio is sinθ. Find the number of solutions of the equation, G=G' in [0,2π] is
View Solution
Knowledge Check
If x,y and b are real numbers and x<y,<0, then
Axb<ybBxb≤ybCxb>ybDxb≥ybFind the first term of a G.P., whose 8th term is 192 and common ratio is 2.
A32B23C3D2The fifth term of a G.P. is 32 and common ratio is
2 , then the sum of first 14 terms of the G.P. isA16388B32667C32766D64342
The sum to infinity of a G.P.is 4 times the first term.Then the common ratio
View SolutionThe first four terms of an AP whose first term is 3x+y and common difference is x−y are
View SolutionConsider the infinite geometric series with first term a and common ratio r If its sum is '4' and second term is 34 then Sum of 10 terms of the series is
View SolutionThe sum of some terms of G. P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
View SolutionThe sum of some terms of a G.P. is 315 whose first term and the common ratio are 5 and 2, respectively. Find the last term and the number of terms.
View Solution
