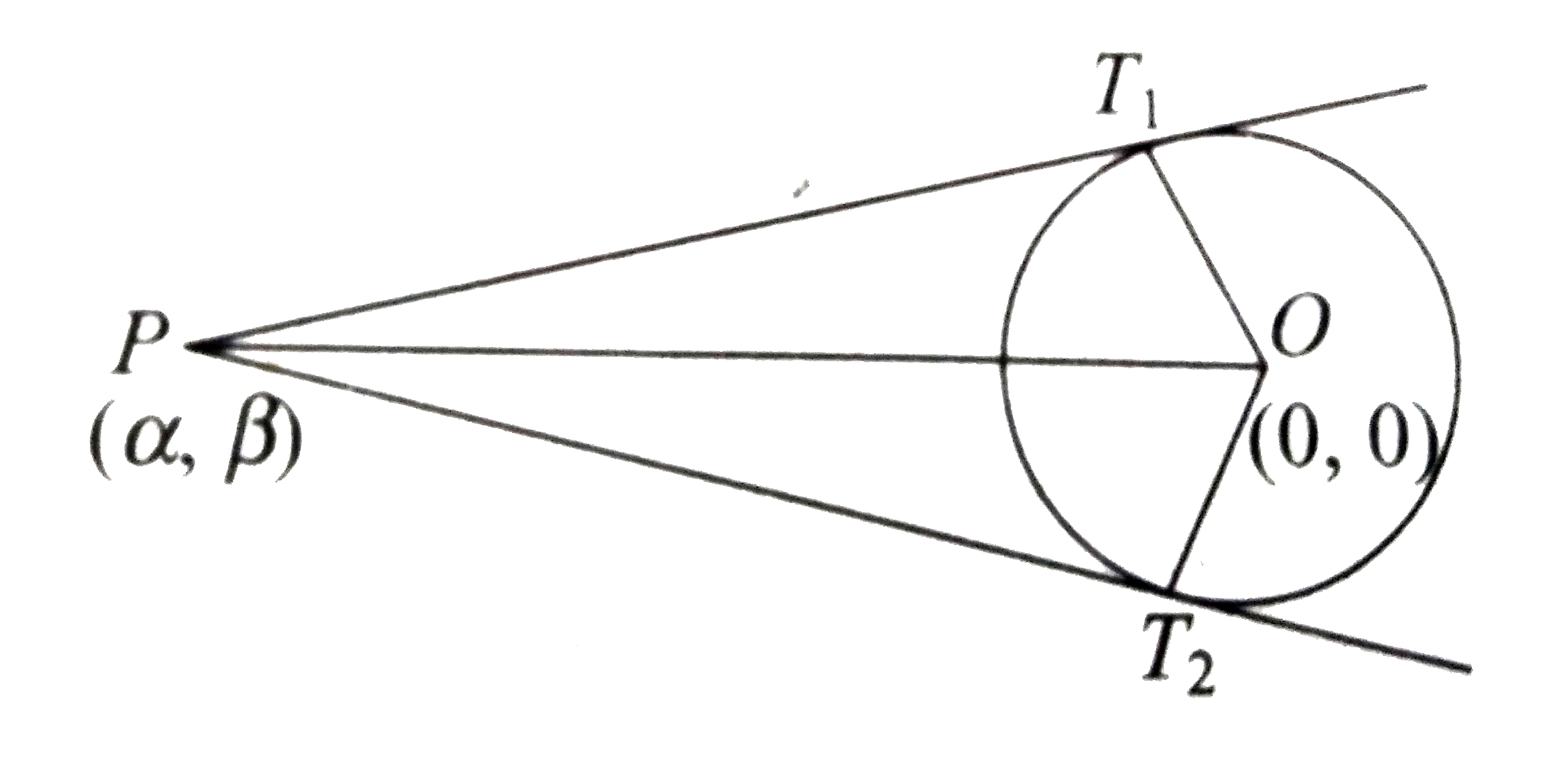
Tangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
px+qy=r
(x−p)2+(y−q)2=r2
px+qy=r2
2px+2qy+r=0
The correct Answer is:D
P,T2,Q,T1 are concylic points with PO as diameter.
Thus, the circumcentre of ΔPT1T2 is (α2,β2).
New (α,β) lies on px+qy+r=0
i.e, locus of (α2,β2) is 2px+2qy+r=0.
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Tangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionTangents PA and PB are drawn from a point P to the circle x2+y2−2x−2y+1=0. If the point plies on the line lx+my+n=0, where l,m,n are constants, then find the locus of the circum-Centre of the ΔPAB.
View Solution
Knowledge Check
Tangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
Ax2+y2+4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−20Dx2+y2−6x−4y+19=0A pair of tangents are drawn from a point P to the circle x2+y2=1. If the tangents make an intercept of 2 on the line x=1, the locus of P is
Astraight lineBpair of linesCcircleDparabolaTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B the equation of the circumcircle of △PAB is
Ax2+y2÷4x−6y+19=0Bx2+y2−4x−10y+19=0Cx2+y2−2x+6y−29=0Dx2+y2−6x−4y+19=0
A pair of tangents are drawn from a point P to the circle x2+y2=1. If the tangents make an intercept of 2 on the line x=1 then the locus of P is
View SolutionTangents PA and PB are drawn to the circle (x+3)2+(y−4)2=1 from a variable point P on y=sinx. Find the locus of the centre of the circle circumscribing triangle PAB.
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View SolutionTangents drawn from the point P (1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A and B. The equation of the circumcircle of the triangle PAB is:
View Solution
