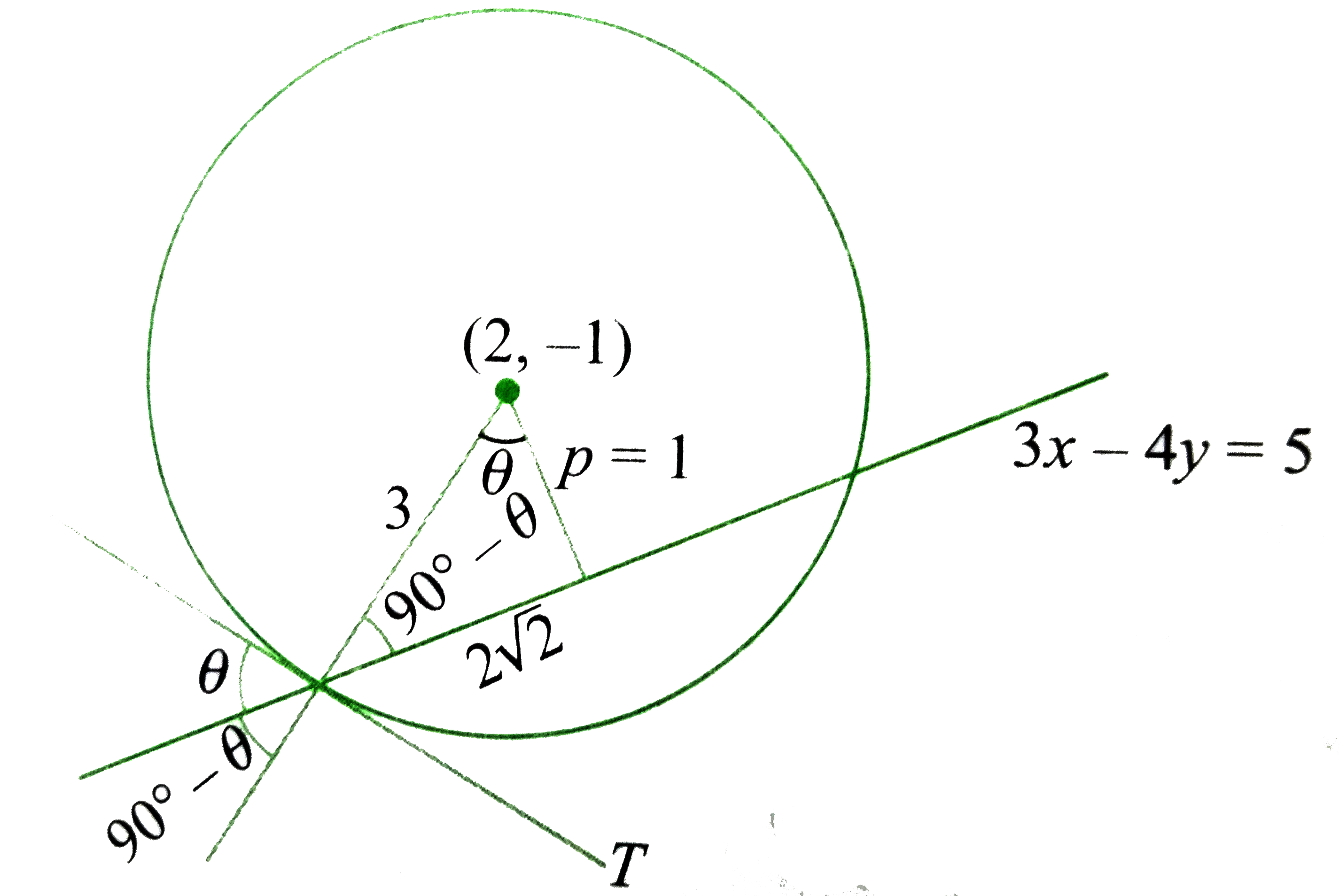
The acute angle between the line $3 x - 4 y = 5$ and the circle $x^{2} + y^{2} - 4 x + 2 y - 4 = 0$ is $θ$ . Then $9 cos θ =$

Text Solution

Verified by Experts

The correct Answer is:3

$θ$ is the angle between the tangent and the line
The circle has center $(2, - 1)$ and radius 3.
The length of perpendicular from the center on $3 x - 4 y = 5$ is
$p = ∣ ∣ ∣ \frac{6 + 4 - 5}{5} ∣ ∣ ∣ = 1$
or $sin (90 - θ) = \frac{1}{3}$
or $cos θ = \frac{1}{3}$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The acute angle between the line represented by $2 x^{2} + x y - y^{2} + x + 4 y - 3 = 0$ is
A ${tan}^{- 1} 3$
B ${tan}^{- 1} 5$
C ${tan}^{- 1} (2 \sqrt{3})$
D ${tan}^{- 1} (2 \sqrt{2})$
Question 2 - Select One
The acute angle between the line represented by $x^{2} - 6 x y + 5 y^{2} + 10 x - 4 y + 9 = 0$ is
A ${tan}^{- 1} (\frac{3}{2})$
B ${tan}^{- 1} (\frac{3}{4})$
C ${tan}^{- 1} (\frac{2}{3})$
D ${tan}^{- 1} (\frac{4}{3})$
Question 3 - Select One
The acute angle $θ$ between the lines represented by $4 x^{2} + 5 x y + y^{2} = 0$ is
A ${tan}^{- 1} (\frac{1}{5})$
B ${tan}^{- 1} (\frac{1}{3})$
C ${tan}^{- 1} (\frac{3}{5})$
D ${tan}^{- 1} (\frac{5}{3})$

CENGAGE-CIRCLE -Exercise (Numerical)

Home
Ask Doubt
Profile