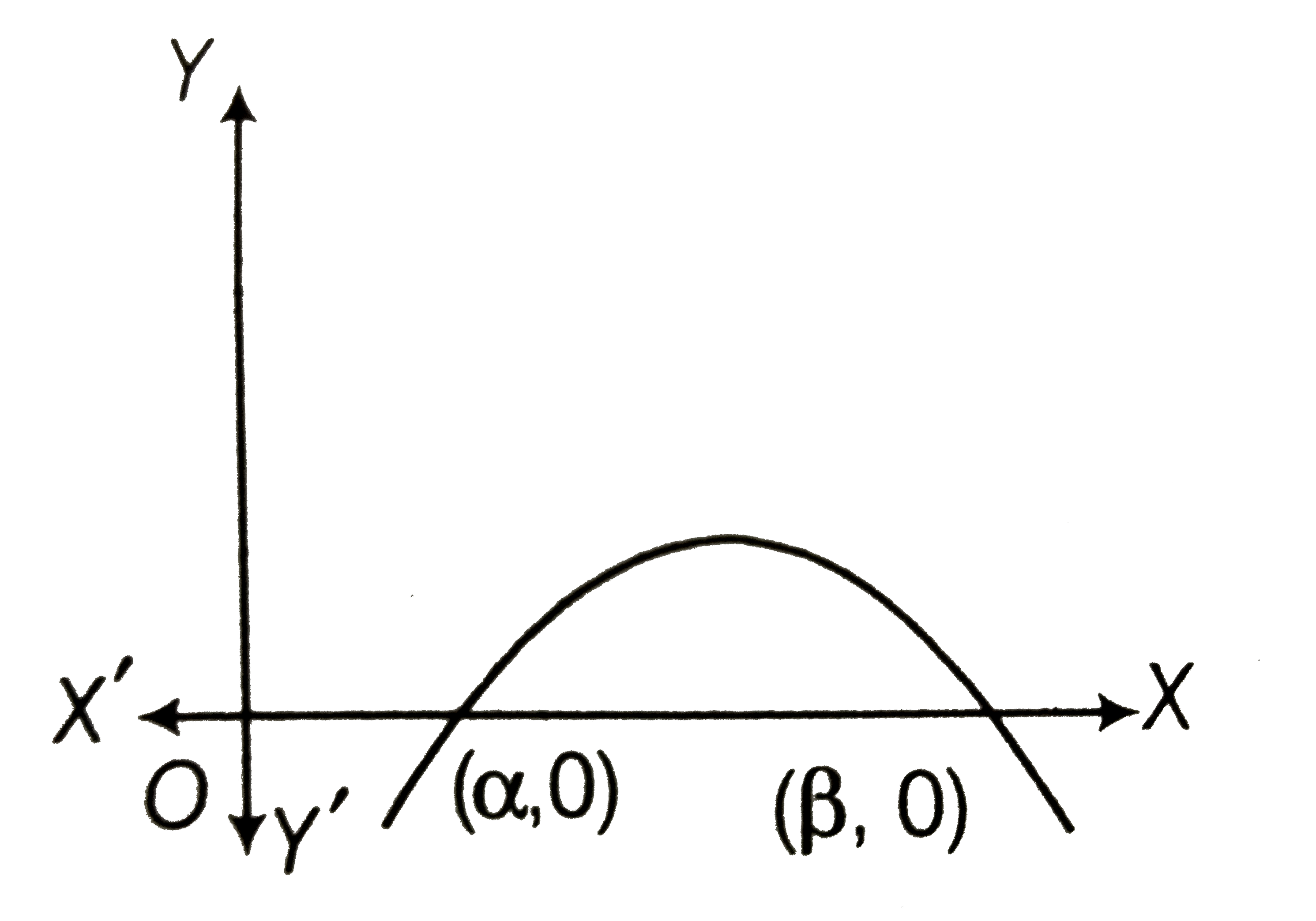
The adjoining graph of $y = a x^{2} + b x + c$ shows that
Solution in Gujrati

A

$a < 0$

B

$b^{2} < 4 a c$

C

$c > 0$

D

a and b are of opposite signs

Video Solution

Text Solution

Verified by Experts

The correct Answer is:A, D

It is clear from graph that the equation $y = a x^{2} + b x + c = 0$ has two real and distinct roots. Therefore
$b^{2} - 4 a c > 0$ ………..i

$∴$ Parabola open downwards.
$a < 0$
and $y = a x^{2} + b x + c$ cuts off $Y$ axis at $x = 0$
$∴ y = c < 0$
$\Rightarrow c < 0$
and x-coordinate of vertex $> 0$
$\Rightarrow - \frac{b}{2 a} > 0 \Rightarrow \frac{b}{a} < 0$
$\Rightarrow b > 0 [∵ a < 0]$
It is clear that a and b are of opposite signs.

Updated on:21/07/2023

|

Class 12 MATHS QUADRATIC EQUATIONS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile