The altitude AD of a ABC, in which ∠A obtuse and, AD=10cm. If BD=10cmandCD=10√3cm, determine ∠A.
60∘
30∘
105∘
None of these
The correct Answer is:C
Step by step video, text & image solution for The altitude A D of a A B C , in which /_A obtuse and, A D=10c mdot If B D=10 c ma n dC D=10sqrt(3)c m , determine /_Adot by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIGNOMETRIC RATIOS BOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TRIGNOMETRIC RATIOS EXERCISE - Exam Booster for Cracking Exam
25 Videos
- TIME AND WORKBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TIME AND WORKEXERCISE - Exam Booster for Cracking Exam
18 Videos
- TRIGONOMETRIC IDENTITIESBOOK - ARIHANT PUBLICATION JHARKHANDCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - EXAM BOOSTER FOR CRACKING EXAM
35 Videos
Similar Questions
The altitude AD of a ΔABC, in which ∠A obtuse and, AD=10cm. If BD=10cm and CD=10√3cm, determine ∠A.
View SolutionIn Fig. 4.60, check whether AD is the bisector of ∠A of ABC in each of the following: (FIGURE) AB=5cm, AC=10cm, BD=1.5cm and CD=3.5cm (ii) AB=4cm, AC=6cm, BD=1.6cm and CD=2.4cm (iii) AB=8cm, AC=24cm, BD=6cm and BC=24cm
View SolutionP is the mid-point of side BC of a parallelogram ABCD such that ∠BAP=∠DAP. If AD=10cm, then CD= 5cm (b) 6cm (c) 8cm (d) 10cm
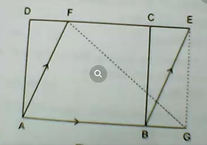
View SolutionIn Figure, ABCD is a rectangle with sides AB=10cmandAD=5cm Find the area of EFG
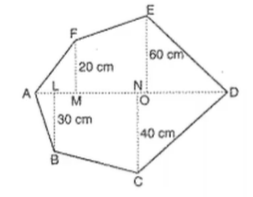
View SolutionFind the area of the following polygon, if AL=10cm, AM=20cm, AN=50cm, AO=60cm and AD=90cm.
View SolutionIn Fig.20, ABCD is a parallelogram, DL⊥AB and DM⊥BC. If AB=18 cm , BC=12 cm and DM=9.3 cm, find DL.
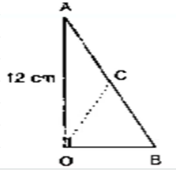
View SolutionIn Figure, ∠AOB=900, AC=BC, OA=12 cm and OC=6.5cm. Find the area of AOB.
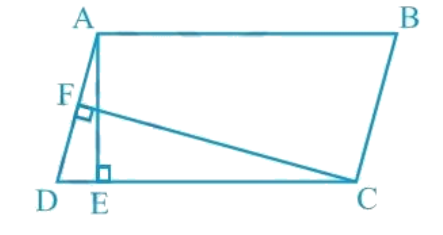
View SolutionIn Figure, ABCD is a parallelogram, AE ⊥DC and CF⊥AD . If AB=16CM, AE=8cm and CF=10cm, find AD
View SolutionIn fig. 15 ABCD is a parallelogram CM⊥AB and BL⊥AD. If AB=16 cm, AD=12 cm, CM=10 cm, find BL If AD=10cm, CM=8cm, BL=12 cm, find AB .
View SolutionIn a ΔABC, if b=√3, c=1 and ∠A=300, then find a
View Solution
