The angle between a pair of tangents from a point P to the circe $x^{2} + y^{2} + 4 x - 6 y + 9 sin 2 α + 13 {cos}^{2} α = 0$ is $2 α$ . Find the equation of the locus of the point P.

A

$x^{2} + y^{2} + 4 x - 6 y + 4 = 0$

B

$x^{2} + y^{2} + 4 x - 6 y - 9 = 0$

C

$x^{2} + y^{2} + 4 x - 6 y - 4 = 0$

D

$x^{2} + y^{2} + 4 x - 6 y + 9 = 0$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:4

The center of the circle
$x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$
is $C (- 2, 3)$ and its radius is
$\sqrt{4 + 9 - 9 {sin}^{2} α - 13 {cos}^{2} α} = | 2 sin α |$

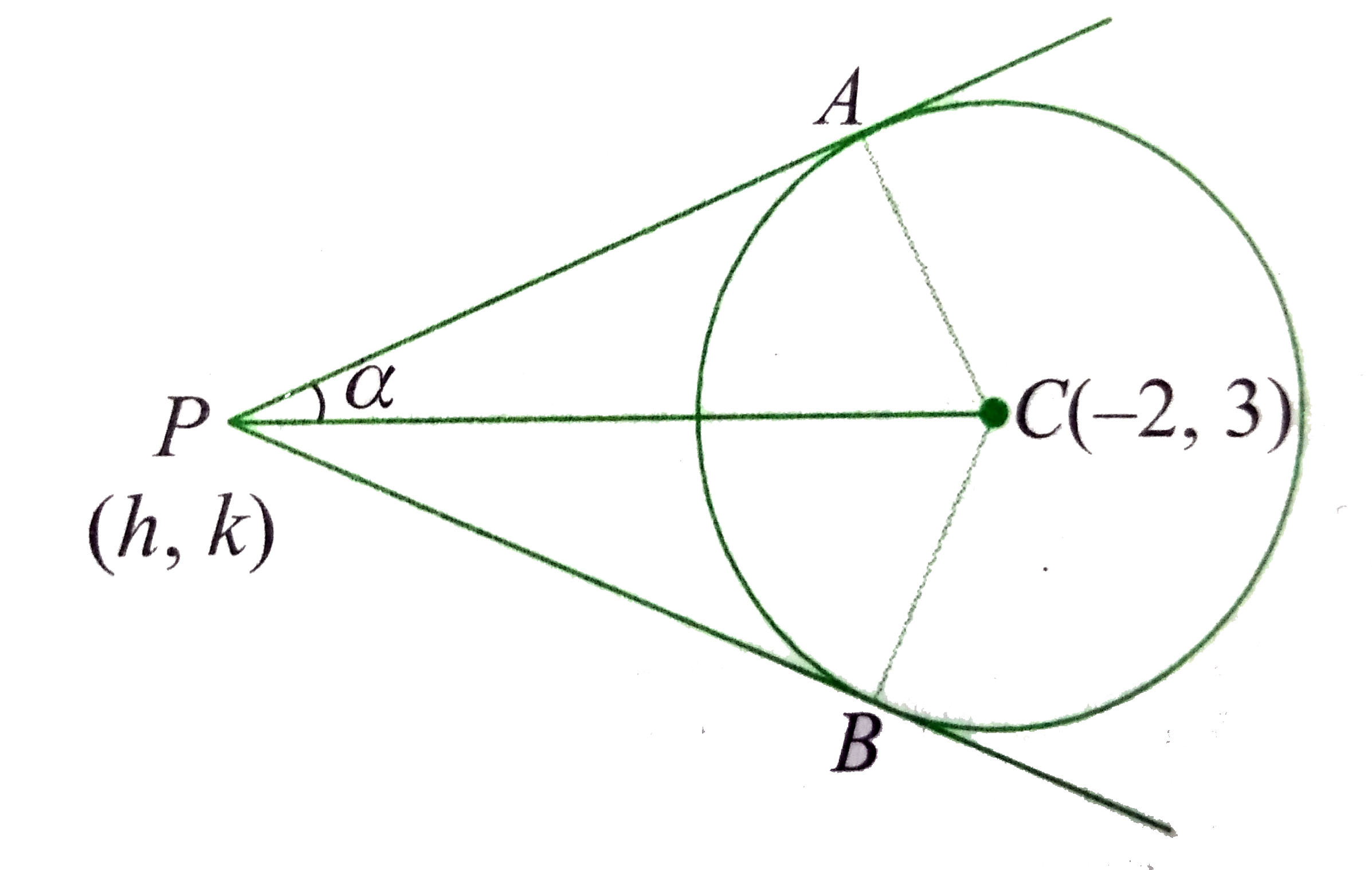
Let $P (h, k)$ be any point on the locus . Then $∠ A P C = α$
From the diagram,
$sin α = \frac{A C}{P C} = \frac{2 sin α}{\sqrt{{(h + 2)}^{2} + {(k - 3)}^{2}}}$
or ${(h + 2)}^{2} + {(k - 3)}^{2} = 4$
or $h^{2} + k^{2} + 4 h - 6 k + 9 = 0$
Thus, the required equation of the locus is
$x^{2} + y^{2} + 4 x - 6 y + 9 = 0$

|

Updated on:21/07/2023

Class 12 MATHS CIRCLE

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
The angle between the pair of tangents drawn from a point $P$ to the circle $x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$ is $2 α$ . then the equation of the locus of the point $P$ is $x^{2} + y^{2} + 4 x - 6 y + 4 = 0$ $x^{2} + y^{2} + 4 x - 6 y - 9 = 0$ $x^{2} + y^{2} + 4 x - 6 y - 4 = 0$ $x^{2} + y^{2} + 4 x - 6 y + 9 = 0$
Aa. $x^{2} + y^{2} + 4 x - 6 y + 4 = 0$
Bb. $x^{2} + y^{2} + 4 x - 6 y - 9 = 0$
Cc. $x^{2} + y^{2} + 4 x - 6 y - 4 = 0$
Dd. $x^{2} + y^{2} + 4 x - 6 y + 9 = 0$
Question 2 - Select One
The angle between a pair of tangents drawn from a point T to the circle $x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$ is . The equation of the locus of the point T is
A $x^{2} + y^{2} + 4 x - 6 y + 4 = 0$
B $x^{2} + y^{2} + 4 x - 6 y - 9 = 0$
C $x^{2} + y^{2} + 4 x - 6 y - 4 = 0$
D $x^{2} + y^{2} + 4 x - 6 y + 9 = 0$
Question 3 - Select One
The locus of a moving point so that tangents from it to circle $x^{2} + y^{2} + 4 x - 6 y + 9 {sin}^{2} α + 13 {cos}^{2} α = 0$ are inclined at an angle $' 2 α'$ Find the equation of the locus of the point . :
A $y^{2} = 4 (x + 2)$
B $x^{2} + y^{2} + 4 x - 6 y + 9 = 0$
C $x^{2} + y^{2} + 4 x - 6 y - 9 = 0$
D $3 x^{2} + 2 y^{2} = 12$

CENGAGE-CIRCLE -Exercise (Single)

Home
Ask Doubt
Profile