The angle of elevation of the top of a tower at a point on a level ground is 30°.After walking a distance of 100mtowards the foot of the tower along the horizontal line through the foot of the tower on the same level ground, the angle of elevation of the top of the tower is 60°.Find the height of the tower.Solution in Assamese
Step by step video & image solution for The angle of elevation of the top of a tower at a point on a level ground is 30°.After walking a distance of 100mtowards the foot of the tower along the horizontal line through the foot of the tower on the same level ground, the angle of elevation of the top of the tower is 60°.Find the height of the tower. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
Similar Questions
Solve by the method of elimination:
5x−3y=1,2x+5y=19
View Solution△ABC~△DEF and their areas are respectively 64 cm2 and 121 cm2. If EF=14.4cm find BC.
View SolutionThe angle of elevation of the top of a tower at a point on the line through the foot of the tower is 45^(@). After walking a distance towards the foot of the tower along the same horizontal line elevation of the top of the tower changes to 60^(@). Find the height of tower.
View SolutionA person observed the angle of elevation of the top of a tower as 30∘ . He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60∘ . Find the height of the tower.
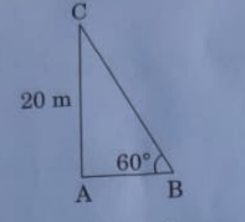
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionThe angle of elevation of the top of a tower at a point on the level ground is 30°. After walking a distance of I 00 m towards the foot of the tower along the horizontal line through the foot of the tower on the same level ground, the angle of elevation of the top of the tower is 60°. Find the height of the tower.
View SolutionFrom a point on the ground 40m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘ . The angle of elevation of the top of a water tank (on the top of the tower) is 45∘ . Find the (i) height of the tower (ii) the depth of the tank.
View SolutionA tower stands vertically on the ground. From a point on the ground, 20m away from the foot of the tower, the angle of elevation of the top of the tower is 60∘ . What is the height of the tower?
View SolutionA person observed the angle of elevation of the top of a tower as 30∘ . He walked 50m towards the foot of the tower along level ground and found the angle of elevation of the top of the tower as 60∘ . Find the height of the tower.
View SolutionThe angle of elevation of the top of a tower from a point on the ground 30m away from the foot of the tower is 30∘. Then, the height of the tower is ……..m
View SolutionThe angle of elevation of the top of a tower from a point A on the ground is 30∘. On moving a distance of 20 metres towards the foot of the tower to a point B, the angle of elevation increases to 60∘. Find the height of the tower and distance of the tower from the point A.
View SolutionFrom a point on the ground 40 m away from the foot of a tower, the angle of elevation of the top of the tower is 30∘. The angle of elevation to the top of a water tank (On the top of the tower) is 45∘. Find the height of the tower and the depth of the tank.
View SolutionA person observed the angle of elevation of the top of a
tower as 30∘. He walked 50m towards the foot of the tower
along level ground and found the angle of elevation of the top
of the tower as 60∘ . Find the height of the tower.
View SolutionIn figure, the angle of elevation of the top of a tower AC from a point B on the ground is 60∘. If the height of the tower is 20m , find the distance of the point from the foot of the tower.
View SolutionThe angle of elevation of a tower from a point on the same level as the foot of the tower is 30∘ on advancing 150 meters towarsd the foot of the tower, the angle of elevation of the tower becomes 60∘. Find the height of the tower.
View Solution
